基础概念
半监督学习介于监督学习与无监督学习之间。一般而言，半监督学习的任务与监督学习一致，任务中包含有明确的目标，如分类。而所采用的数据既包括有标签的数据，也包括无标签的数据。
前置知识
香农熵
\(H(X)=\sum_{x} P(x) \log _{2}[P(x)]\) 变量的不确定性越大，熵就越大，把变量弄清楚所需要的信息量也就越大。
熵正则化
熵正则化：就是在似然函数的基础上，再加上香农熵，值得注意的是，似然 函数的范围是 已经标记的数据，香农熵的范围是未标记的数据。 \(C = \sum_{i=1}^{l} \ln P\left(y_{i} \mid x_{i} ; \theta\right) + \lambda \sum_{x} P(x) \log _{2}[P(x)]\)
类间的低密度分离
低密度分离的假设就是假设数据非黑即白，在两个类别的数据之间存在较为明显的鸿沟，即在两个类别之间的边界数据的密度很低（数据质量很好）
Self-training
首先基于有标签的数据训练一个模型，然后将没有标签的数据输入进去进行预测，得到没有标签数据的一个标签，之后将一部分的带有伪标签的数据转移到有标签的数据中，再进行训练，循环往复。如何选取加入有标签数据的伪标签数据需要自己定义。
平滑性假设
数据的分布是不均匀的，有的地方比较稀疏，有的地方比较密集。 如果在高密度的地方比较相近，则两个数据具有相同的标签 精神：近朱者赤、近墨者黑
Denosing Auto-Encoder
以一定的概率分布去擦除原始的input矩阵（这样看起来是丢失了部分数据）。以这丢失的数据去计算y，计算z，并将z和原始x做误差迭代，这样网络就学习了这个破损的数据。这样的破损数据有用。
1
2
1.通过与非破损数据训练的对比，破损数据训练出来的weight噪声比较小，降噪因此的名
2.破损数据一定程度上减轻了训练数据与测试数据之间的代沟，由于数据的部分被丢弃了，因而破损数据一定程度上比较接近测试数。
最小熵
“知识”有一个固有信息熵，代表它的本质信息量。但在我们彻底理解它之前，总会有未知的因素，这使得我们在表达它的时候带有冗余，所以按照我们当前的理解去估算信息熵，得到的事实上是固有信息熵的上界，而信息熵最小化意味着我们要想办法降低这个上界，也就意味着减少了未知，逼近固有信息熵。
MixUp
假设有两个样本$\left(x_{i}, y_{i}\right),\left(x_{j}, y_{j}\right)$,做如下处理： \(\begin{array}{l} \tilde{x}=\lambda x_{i}+(1-\lambda) x_{j} \\ \tilde{y}=\lambda y_{i}+(1-\lambda) y_{j} \end{array}\) 将$(\tilde{x}, \tilde{y})$作为增强数据或者虚拟训练数据，可以提高模型的鲁棒性和泛化能力。
主流方法
Pseudo-Label
主要的思想
1
2
1.运用训练出的模型给予无标签的数据一个伪标签
2.运用熵正则化思想，将无监督数据转化为目标函数的正则项。
总体的损失函数为： \(L=\frac{1}{n} \sum_{m=1}^{n} \sum_{i=1}^{C} L\left(y_{i}^{m}, f_{i}^{m}\right)+\alpha(t) \frac{1}{n^{\prime}} \sum_{m=1}^{n^{\prime}} \sum_{i=1}^{C} L\left(y_{i}^{m}, f_{i}^{\prime m}\right)\) n表示SGD中有标签数据的mini-batch大小 $n’$表示SGD中无标签数据的mini-batch大小 $f_i^m$表示有标签数据中m个样本的输出集合 $y_i^m$表示有标签数据中m个样本的真实标签 $f_i^{\prime m}$是无标签数据中m个样本的输出集合 $y_i^{\prime m}$是无标签数据中m个样本的伪标签 $\alpha (t)$是平衡他们的系数
不足：
1
2
Pseudo-Label 方法只在训练时间这个维度上，采用了退火思想，即采用时变系数α(t)。而在伪标签这个维度，对于模型给予的预测标签一视同仁,这就会引入错误信号。
假如模型对某一个样本所 预测的几个类别具有类似的低概率，每个都是0.1左右，那再以最大概率对应的的类别为伪标签，就不太合适。
Γ Model
主要思想：
1
2
作者认为，监督学习与无监督学习存在一定程度的冲突，无监督学习希望尽可能的保留原始信息，监督学习希望保留与监督任务相关的信息，对于其他与任务无关的特征并不关心。
半监督学习应该兼顾这两点。
Ladder Network结构：
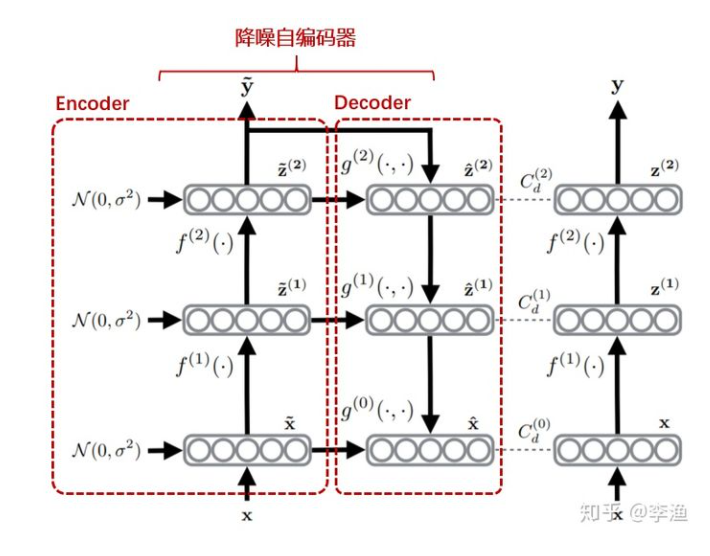
如上图，网络由两部分组成，分别是降噪自编码器以及无噪的前向网络（一般与降噪自编码器的编码端相同）。 对于有标签数据，数据只会流经降噪自编码器的 Encoder 模块，并通过顶层的输出与原始输入构建有监督的目标函数。 对于无标签数据，数据经过编码模块实现加噪编码，随后经过解码模块进行逐层解码，并获取一系列隐层表示，分别是$\tilde{z}^{(1)}, \quad \tilde{z}^{(2)}$等。另一方面，最右侧的无噪前向网络也会对原始无标签数据进行逐层解码得到$z^{(1)}, z^{(2)}$，这正是解码端对应隐层的目标值，通过极小化均方差误差，既可以从无标签数据中提取到学习信号。
整体的目标函数为： \(\begin{aligned} C &=C_{\mathrm{c}}+C_{\mathrm{d}} \\ &=-\frac{1}{N} \sum_{n=1}^{N} \log P(\tilde{\mathbf{y}}=t(n) \mid \mathbf{x}(n))+\sum_{l=0}^{L} \frac{\lambda_{l}}{N m_{l}} \sum_{n=1}^{N}\left\|\mathbf{z}^{(l)}(n)-\hat{\mathbf{z}}_{\mathrm{PA}}^{(l)}(n)\right\|^{2} \end{aligned}\) 第一项为有标签loss，第二项为无标签loss
Π Model & Temporal ensembling Model
Π Model
核心在于利用一致性正则从无标签的数据中提取有效信号。一致性正则表达了一种先验，即网络再输入数据的附近空间应该是平坦的，即使输入数据发生微弱变化，模型的输出也能够基本保持不变。
\(\operatorname{loss} \leftarrow-\frac{1}{|B|} \sum_{i \in(B \cap L)} \log z_{i}\left[y_{i}\right]+w(t) \frac{1}{C|B|} \sum_{i \in B}\left\|z_{i}-\tilde{z}_{i}\right\|^{2}\)
注意公式中的L为有标签数据、B为minbatch，C为类别数目
1
2
1. 对每一个训练样本，在训练阶段进行两次前向计算，一次是随机增强变化，一次是模型的前向运算。由于增强是随机的，同时模型采用dropout，这两个因素都会造成两次前向运算结果的不同。
2. 损失函数由两部分构成，一种是交叉熵 ，一种是两次前向运算的均方误差。
Temporal ensembling Model
相较于Π Model，不同点在于目标函数的无监督loss项，Π Model计算的是两次前向结果的均方差，Temporal ensembling采用的是当前模型预测结果与历史预测结果的平均值做均方差计算。
这样做的好处：
1
2
用空间换时间，在相同的epoch下，总的前向计算次数少了一半，训练速度加快
通过历史预测做平均，有利于平滑单次预测中的噪声
VAT
VAT与Temporal ensembling Model 思想基本一致，都是想表示，模型所描述的系统是光滑的，因此当输入数据发生微小变化的i时候，模型的输出变化应该也是微小的，进而预测的标签是近似不变的。
VAT使用的噪声是模型变化最陡峭方向上的噪声，也就是所谓的对抗噪声，作者认为，如果模型在对抗噪声下，依然能够保持平滑，那么整个网络就能够表现出很好的一致性。
损失函数： \(\begin{array}{r} L_{\mathrm{adv}}\left(x_{l}, y_{l}, \theta\right):=D\left[h\left(y_{l}\right), p\left(y \mid x_{l}+r_{\mathrm{adv}}, \theta\right)\right] \\ \text { where } r_{\mathrm{adv}}:=\underset{r ;\|r\| \leq \epsilon}{\arg \max } D\left[h\left(y_{l}\right), p\left(y \mid x_{l}+r, \theta\right)\right] \end{array}\) 其中$r_{adv}$表示对输入数据所施加的对抗噪声，D表示模型对施加噪声前后两个输入对应输出的度量，这里采用的是KL三散度。 \(D[p(y \mid x), p(y \mid x+r)]:=\sum_{y \in Q} p(y \mid x) \log \frac{p(y \mid x)}{p(y \mid x+r)}\) 最后在损失函数中还加入了第三项，entropy minimization 项。即要求模型无论对于有标签数据还是无标签数据，都要求其熵尽可能小。 \(\mathcal{R}_{\text {cent }}=H(Y \mid X)=-\frac{1}{N_{l}+N_{u l}} \sum_{x \in \mathcal{D}_{l}, \mathcal{D}_{u l}} \sum_{y} p(y \mid x, \theta) \log p(y \mid x, \theta)\) 这和Pseudo-Label 模型中的第二项一样。
Mean Teacher
Mean Teacher由Temporal ensembling Model 发展而来，主要解决了其中两个问题（无标签数据的信息只能在下一次 epoch 时才能更新到模型）：
1
2
1. 大数据集下，模型更新缓慢
2. 无法实现模型在线训练
核心思想：
1
模型既充当学生，又充当老师。作为老师，用来产生学生学习时的目标；作为学生，则利用教师模型产生的目标来进行学习。而教师模型的参数是由历史上(前几个step)几个学生模型的参数经过加权平均得到
损失函数：
\(\mathcal{L}=w \frac{1}{\left|\mathcal{D}_{u}\right|} \sum_{x \in \mathcal{D}_{u}} d_{\operatorname{MSE}}\left(f_{\theta}(x), f_{\theta^{\prime}}(x)\right)+\frac{1}{\left|\mathcal{D}_{l}\right|} \sum_{x, y \in \mathcal{D}_{l}} \mathrm{H}\left(y, f_{\theta}(x)\right)\)
其中$\theta$ 的更新为：
\(\theta_{t}^{\prime}=\alpha \theta_{t-1}^{\prime}+(1-\alpha) \theta_{t}\)
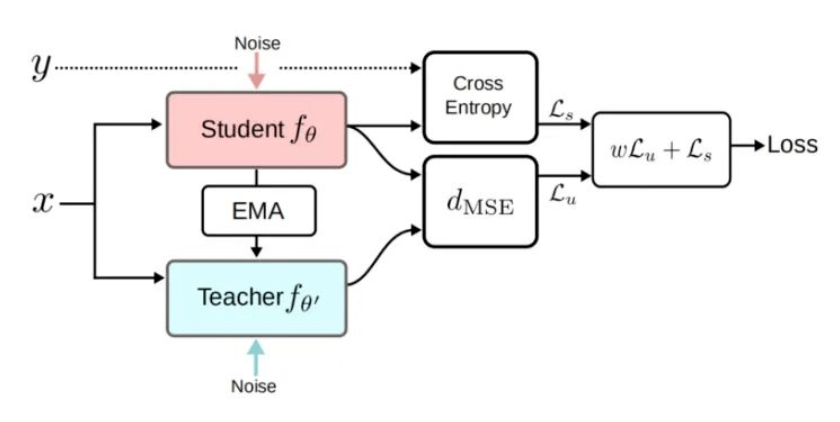
由此可知，Mean teacher相对比于 temporal ensembling的优势在于：
1
2
1. 在temporal ensembling中，无标签数据的目标标签来自模型前几个epoch预测结果的加权平均。而在Mean Teacher中，无标签数据的目标标签来自teacher模型的预测结果。
2. 由于是通过模型参数的平均来实现标签预测，因此在每个step都可以把无标签中的信息更新到模型中，而不必像temporal ensembling模型需要等到一个epoch结束再更新。这一特点使得这一算法可以用在大数据集以及在线模型上。
MixMatch
融合上述几个方法的精华，一致性正则、伪标签、熵正则化以及Mixup技术。 思想核心：
1
2
1. 伪标签生成，想比较与早期的Pseudo-Label 模型，做了改进。一个是运用数据增强技术对无标签数据进行k次变换，模型分别对k次变换进行预测，然后取k次结果的平均作为伪标签的期望结果。二，在一的基础上，运用熵正则化思想，对于k次平均后的结果，再进行锐化操作，使得各个类别熵的概率值差别更为明显。
2. 数据的MixUp：mixup按照一定比例将有标签的数据进行混合以构成新的样本。Mixup变化本身视为一种正则化技术。直观来看，它要求，当模型的输入为另外两个输入的线性组合时，其输出也是这两个数据单独输入模型后，所得输出的线性组合。
目标函数： \(\begin{aligned} \mathcal{L} &=\mathcal{L}_{\mathcal{X}}+\lambda_{\mathcal{U}} \mathcal{L}_{\mathcal{U}} \\ &=\frac{1}{\left|\mathcal{X}^{\prime}\right|} \sum_{x, p \in \mathcal{X}^{\prime}} \mathrm{H}(p, \text { pmodel }(y \mid x ; \theta))+\lambda_{\mathcal{U}} \frac{1}{L\left|\mathcal{U}^{\prime}\right|} \sum_{u, q \in \mathcal{U}^{\prime}}\left\|q-\mathrm{p}_{\text {model }}(y \mid u ; \theta)\right\|_{2}^{2} \end{aligned}\) 第一项为交叉熵，用于计算有标签数据的误差，第二项为MSE，用于计算无标签数据与伪标签之间的均方误差。
ReMixMatch
相比较于MixMatch做了如下改进：
1
2
1. Distribution Alignment由于MixMatch的标签猜测有可能存在噪声和不一致的情况，作者提出利用有标签数据的标签分布，对无标签猜测进行对齐。
2. Augmentation Anchor：作者的假设是对样本进行简单增强（比如翻转和裁切）之后的预测结果，要比多次复杂变换更加可靠和稳定。因此，对于同一张图片，首先进行弱增强，得到预测结果，然后对同一张图片进行复杂的强增强。弱增强和强增强共同使用一个标签猜测进行Mixup和模型训练。
\(\tilde{q}=\operatorname{Normalize}\left(q \times \frac{p(y)}{\tilde{p}(y)}\right)\) 其中$p(y)$为有标签数据的标签分布，$\tilde{q}$是一个运行平均版本的无标签猜测，q是对当前标签数据的标签猜测。
UDA
从下图的结构上看UDA和 Π Model 基本一致，区别在于无监督loss中一个用的是KL散度一个用的是MSE。
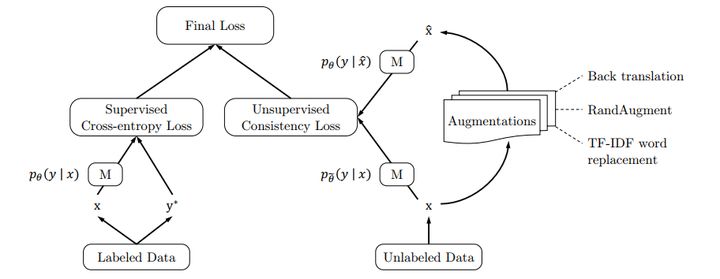
其先进的原因：
1
2
3
1. 采用了先进的数据增强技术，cv领域的RandAugment，NLP领域的Back Translation和非核心词替换。
2. 采用了最新的迁移模型。
3. 采用了一系列精心设计的训练技巧，平衡有监督和无监督的TSA，基于熵正则化锐化技术，无标签数据的二次筛选等。
FixMatch
做了两个简化：
1
2
1. temperature sharpening 换成 pseudo label
2. 通过设定一个阈值，在计算 unlabeled loss 时，对 prediction 的 confidence 超过阈值的 unlabeled instance 才算入 unlabeled loss，这样使得 unlabeled loss 的权重可以固定
损失函数由两部分构成： \(\ell_{s}=\frac{1}{B} \sum_{b=1}^{B} \mathrm{H}\left(p_{b}, p_{\mathrm{m}}\left(y \mid \alpha\left(x_{b}\right)\right)\right) \\ \ell_{u}=\frac{1}{\mu B} \sum_{b=1}^{\mu B} \mathbb{1}\left(\max \left(q_{b}\right) \geq \tau\right) \mathrm{H}\left(\hat{q}_{b}, p_{\mathrm{m}}\left(y \mid \mathcal{A}\left(u_{b}\right)\right)\right)\)
最后的损失函数为$l_s + \lambda _u l_u$，其中$\lambda _u$是一个超参数，表示未标记损失的相对权重。
mixtext
第一步：对未标记数据进行增强，采用未标注数据$X^u$回译进行K次增强生成$X^a$ 第二步：对未标记数据进行标签预测，将原始未标注数据$X^u$和增强后的未标注数据$X^a$一同喂入当前模型中，通过平均加权的方式对未标注数据进行预测。 \(\left.\mathbf{y}_{i}^{u}=\frac{1}{w_{\text {ori }}+\sum_{k} w_{k}}\left(w_{\text {ori }} p\left(\mathbf{x}_{i}^{u}\right)+\sum_{k=1}^{K} w_{k} p\left(\mathbf{x}_{i, k}^{a}\right)\right)\right)\) 由于预测出来的伪标签分布相对平坦，采用Sharpen方式进行锐化 \(\text { Sharpen }(p, T)_{i}:=p_{i}^{\frac{1}{T}} / \sum_{j=1}^{L} p_{j}^{\frac{1}{T}}\) 第三步：对标注数据和未标注数据做TMix，混合在一起生成X然后随机选择两个样本进行TMix，然后通过KL散度计算损失。 \(L_{TMix} = E_{x,x^{\prime} \in X} KL(mix(y, y^{\prime})||p(TMix(x, x^{\prime})))\) 当x的来源不同的时候，上述损失意义不同：
1
2
当x来自目标数据为标注数据时，主要利用来自有标注数据，因此模型损失为有监督损失
当x为无标注数据，主要利用信息来自未标注数据，因此模型损失为一致性训练损失
尴尬的不用标注数据
Text Classification Using Label Names Only: A Language Model Self-Training Approach
