一、数学
1.1、导数
- 概念: \(f \prime (x_0) = lim_{\Delta \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\)
- 函数可导性与连续性之间的关系
- 函数f(x)在\(x_0\)处可导则在\(x_0\)处连续,反之函数连续不一定可导
- 在\(x_0\)处导数存在则左导数等于右导数
- 导数运算规则及常用导数公式
1.1.1、复合函数、反函数的导数
- 复合函数的运算法则:若\(\mu =\varphi (x)\)在点\(x\)可导,而\(y=f(\mu )\)在对应点\(\mu\)(\(\mu =\varphi (x)\))可导,则复合函数\(y=f(\varphi (x))\)在点\(x\)可导,且\({y}'={f}'(\mu )\cdot {\varphi }'(x)\)
- 反函数的运算法则: 设\(y=f(x)\)在点\(x\)的某邻域内单调连续,在点\(x\)处可导且\({f}'(x)\ne 0\),则其反函数在点\(x\)所对应的\(y\)处可导,并且有\(\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}\)
1.1.2、函数单调性的判断
- 函数f(x)在(a, b)区间内可导,如果对\(\forall x\in (a,b)\),都有\(f\prime (x) >0\)或者\(f\prime (x)<0\),则函数在区间内是单调增加或者单调减少
- 取极值的必要条件,函数f(x)在\(x_0\)处可导,且在\(x_0\)处取极值,则\(f(x_0)\prime =0\)
- 函数在\(x_0=0\)处二阶导数不为0,且一阶导数为0,则当二阶导数小于0的时候,在当前点取极大值,当二阶导数大于0的时候,取极小值
2、泰勒公式
- 设函数f(x)在点\(x_0\)处的某个邻域内存在n+1阶导数,则对该邻域内异于\(x_0\)的任一点x,在\(x_0\)于x之间至少存在一个\(\epsilon\),使得: \(f(x) = f(x_0) + f\prime (x_0)(x - x_0) + \frac{1}{2!}f\prime \prime (x_0)(x-x_0)^2 + ... +\frac{f^n (x_0)}{n!}(x-x_0)^n + R_n (x)\)
- 上式中\(R_n(x) = \frac{f^{n+1} \ xi}{(n+1)!}(x-x_0)^{n+1}\)的称为f(x)在\(x_0\)处的n阶泰勒余项
- 令\(x_0=0\),则n阶泰勒公式(麦克劳林公式)为: \(f(x) = f(0) + f\prime (0)(x) + \frac{1}{2!}f\prime \prime (0)(x)^2 + ... +\frac{f^n (0)}{n!}(x)^n + R_n (x)\)
- 知乎解释
3、拉格朗日乘子
3.1、等式约束
- 如果是等式约束直接加入拉格朗日乘子即可:
- 对问题\(maxf(P) = d(M,P) +d(P,C)\)在\(g(P)=0\)的条件下
- 引入\(\lambda\)定义一个新的函数\(F(P, \lambda )= f(P) - \lambda g(P)\)
-
令 \(\nabla F(\boldsymbol{P}, \lambda)=\nabla F(x, y, \lambda)=\left(\begin{array}{c} F_x \\ F_y \\ F_{\lambda} \end{array}\right)=\mathbf{0}\)
- 这就与要求的优化问题等价:因为\(F_{\lambda} = g(P) = g(x,y)=0\)与约束条件等价,并且此时\(F(P, \lambda )= f(P) - \lambda 0= f(P)\),即拉格朗日函数与我们的目标函数取相同值。
3.2、不等式约束
- 将不等式约束优化转化为等式约束优化进而转换为无约束优化
- 例如:\(minf(x), s.t. g(x)<=0\)
- 约束\(g(x)<=0\)称为原始可行性。分情况讨论原始问题:
- \(g(x^*)<0\),最佳解在可行域内部,此时称为内部解,此时约束无效
- \(g(x^*)=0\),最佳解在边界上,称为边界解,此时约束条件有效
- 约束\(g(x)<=0\)称为原始可行性。分情况讨论原始问题:
- 内部解和边界解讨论:
- 内部解:在无约束下,驻点满足\(\nabla f = 0, \lambda=0\)
- 边界解:此时约束变为等式约束,此时\(\nabla f = -\lambda \nabla g\),由于要最小化f,梯度应该要指向可能域的内部(求最小值,梯度指向函数变大的方向),但是\(\nabla g\)指向的是可行域的外部(因为约束是小于等于0),因此\(\lambda >= 0\),称为对偶可行性。
- 因此不管是哪一种,\(\lambda g(x)=0\)恒成立,称为互补松弛性
- 知乎参考
3.3、$KKT$条件
对具有等式或者不等式约束的优化问题: \(minf(x) \\ s.t. g_j(x) <= 0 \\ h_k(x) = 0 \\ \left\{\begin{array}{l} \frac{\partial f}{\partial x_i}+\sum_{j=1}^m \mu_j \frac{\partial g_j}{\partial x_i}+\sum_{k=1}^l \lambda_k \frac{\partial h_k}{\partial x_i}=0,(i=1,2, \ldots, n) \\ h_k(\mathbf x)=0,(k=1,2, \cdots, l) \\ \mu_j g_{j}(\mathbf x)=0,(j=1,2, \cdots, m) \\ \mu_j \geq 0 \end{array}\right.\)
- 上式中第一项为拉格朗日函数、第二项为原始可行性、第三项为对偶可行性、第四项为互补松弛性
- 约束有作用的时候\(u_j>=0,g_j(x)=0\),约束不起作用时\(u_j=0,g_j(x)<0\)
3.4、分析推导
- 假设\(z = f(x,y)\)在条件\(g(x, y)=0\)的添加下,在某点处取极值。则两个函数在此处的梯度平行。
- 也就是向量\((f_x \prime (x_0, y_0), f_y \prime (x_0, y_0))\)与\((g_x \prime (x_0, y_0), g_y \prime (x_0, y_0))\)平行
- 也就是:\(\frac{f_{x}^{\prime}\left(x_{0}, y_{0}\right)}{g_{x}^{\prime}\left(x_{0}, y_{0}\right)}=\frac{f_{y}^{\prime}\left(x_{0}, y_{0}\right)}{g_{y}^{\prime}\left(x_{0}, y_{0}\right)}=-\lambda_{0}\)
- 组合为方程组为:\(\left\{\begin{array}{c} f_{x}^{\prime}\left(x_{0}, y_{0}\right)+\lambda_{0} g_{x}^{\prime}\left(x_{0}, y_{0}\right)=0 \\ f_{y}^{\prime}\left(x_{0}, y_{0}\right)+\lambda_{0} g_{y}^{\prime}\left(x_{0}, y_{0}\right)=0 \\ g\left(x_{0}, y_{0}\right)=0 \end{array}\right.\)
- 也可以引入辅助函数\(L(x, y, \lambda)=f(x, y)+\lambda g(x, y)\),求偏导后和方程组相同。也就是将条件极值问题转化为无条件极值。
4、微分中值定理
- 费马定理:若函数满足
- 函数在某点的邻域内有定义,并且领域内恒有:\(f(x)\le f(x_0)\)或者\(f(x)\ge f(x_0)\)
- 函数在某点处可导,则在该点的一阶导数为0
- 罗马定理:函数满足
- 在闭区间内连续[a, b]
- 在开区间内可导(a, b)
- f(a) = f(b)
- 则(a,b)内存在一个\(\epsilon\)使得一阶导数在该点为0
- 拉格朗日中值定理:
- 在[a,b]上连续
- 在(a,b)内可导
- 则(a,b)内存在\(\epsilon\),使得\(\frac{f(b)-f(a)}{b-a}={f}\prime (\epsilon )\)
- 柯西中值定理:
- 在[a,b]上连续
- 在(a,b)内可导且\(f\prime (x), g\prime (x)\)均存在,且\(g\prime (x) \ne 0\)
- 则:(a,b)内存在一个\(\epsilon\)使得\(\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f\prime (\epsilon )}{g\prime (\epsilon )}\)
5、凹凸性
- 凹凸性判别定理:若在区间内二阶导大于0,则在区间内为凸,反之则为凹
- 拐点判别定理:
- 若函数在某点处二阶导数为0或者不存在,当该点变动经过另外一个点的时候,二阶导数变号,则经过的点为拐点
- 若函数在某点处存在三阶导数,并且三阶导数不为0,同时二阶导数为0,则改点为拐点
- 判断凸函数:
- \(jessenn\)不等式:\(f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y)\)
- 满足\(jensen\)不等式
- 凸集:在欧式空间中,对于集合中的任意两点之间的连线,连线上的点都在集合中,则称之为凸集
6、欧拉公式
- 泰勒公式 \(e^x = 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!}x^3 + ..... \\ sinx = x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - ...... \\ cosx = 1 - \frac{1}{2!} x^2 + \frac{1}{4!} x^4\)
- 结合上面的三个公式得到:\(e^{it} = cos(t) + isin(t)\)
- 当x为\(\pi\)的时候:\(e^{i\pi} + 1 = 0\)
7、傅里叶变换
- 知乎资料,资料二
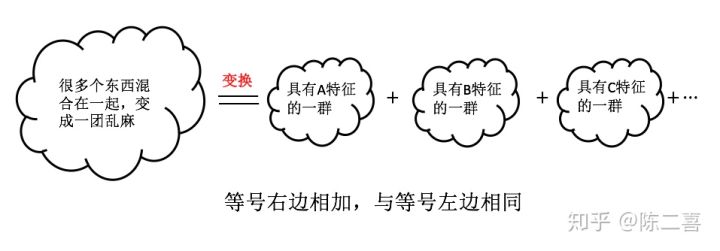
- 将杂乱无章的信息,通过某种信息进行分类筛选
- 从滤波的角度看,将不需要的信息剔除
- 物理层面上:阳光是有频率不同的光线组合而成,通三棱镜后,形成彩虹,这也是傅里叶变
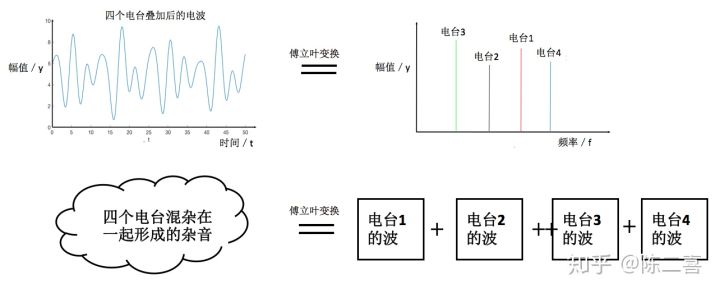
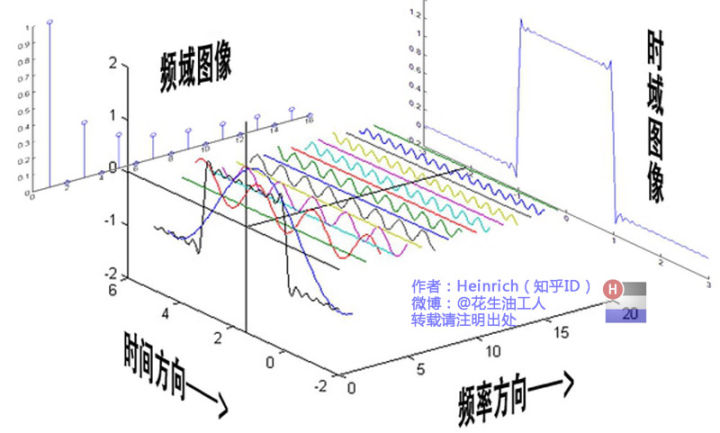
- 傅里叶公式: \(\begin{array}{c} f(t)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} F\left(\omega_{x}\right) \cdot e^{i \omega_{x} t} d \omega_{x} \\ F\left(\omega_{x}\right)=\int_{t_{0}}^{t_{0}+T} f(t) e^{-i \omega_{x} t} d t \end{array}\)
- 注意:周期函数相加还是周期函数
- 定义:f(t)是t的周期函数,如果t满足狄利克雷条件则F(x)以2T为周期的傅里叶级数收敛,和函数S(x)也是以2T为周期的周期函数,且在这些间断点上,函数是有限值,在一个周期内具有有限个极值点,绝对可积,则\(F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt\)成立,称为积分f(t)的傅里叶变换。
- 函数f(x),g(x)在R上绝对可积,则卷积函数\(f*g(x) = \int_{-\infty}^{\infty}f(x-t)f(t)dt\)的傅里叶变换存在,且\(F[f*g] = F[f].F[g]\)
- 傅里叶变换推导1,傅里叶变换推导2
二、概率
2.1、条件概率和边缘概率以及联合概率
- 联合概率:多个条件同时成立,记做:\(P(X=a,Y=b),or.P(a,b)\)
- 边缘概率表示仅与单个变量相关,记做:\(P(X=a),or,P(Y=b)\)
- 联合概率与边缘概率的关系:将其中一个变量的联合概率求和或者积分掉就是另一个变量的边缘概率 \(P(X=a) = \sum_bP(X=a, Y=b)\\ P(Y=b) = \sum_aP(X=a, Y=b)\)
- 条件概率:在给定一个条件的概率下,求解另一个事件发生的概率
- 公式\(P(X=a,given,Y=b)\)
- 在条件Y=b下的X的条件概率分布也是一种X的概率分布,因此穷举X的可取值后,所有这些值对应的概率之和为1
- 公式\(\sum_a P(X=a,given,Y=b)=1\)
- 联合概率、边缘概率与条件概率之间的关系 \(P(X=a|Y=b) = \frac{P(X=a,Y=b)}{P(Y=b)}\)
- 条件联合分布的分解: \(\begin{array}{l} P(a, b | c)=\frac{P(a, b, c)}{P(c)} \\ =\frac{P(a, b, c)}{P(b, c)} \cdot \frac{P(b, c)}{P(c)} \\ =P(a | b, c) P(b | c) \end{array}\)
- 多变的情况下,分解结果不唯一
2.2、期望、方差、协方差、相关性
- 期望:假设g(X)随机变量,则其期望定义为:\(E[g(X)] \triangleq \int_{-\infty}^{\infty} g(x) f_{X}(x) d x\)
- 公式:\(a \in \mathbb{R}, E[a]=a\)
- 公式:\(a \in \mathbb{R},E[af(X)]=aE[f(X)]\)
- 公式:\(E[f(X)+g(X)]=E[f(X)]+E[g(X)]\)
- 方差:描述变量围绕均值的集中程度:\(\operatorname{Var}[X] \triangleq E\left[(X-E(X))^{2}\right]\)
- 公式:\(\begin{aligned} E\left[(X-E[X])^{2}\right] &=E\left[X^{2}-2 E[X] X+E[X]^{2}\right] \\ &=E\left[X^{2}\right]-2 E[X] E[X]+E[X]^{2} \\ &=E\left[X^{2}\right]-E[X]^{2} \end{aligned}\)
- 公式:\(Val[a]=0\)
- 公式:\(Var[af(X)]=a^2Var[f(X)]\)
- 协方差:衡量两个变量的总体误差、方差是协方差中两个变量相同的特殊情况:\(cov(X, Y)= E((X - \mu)(Y - v)) = E(X.Y) - \mu v\)
- 公式:\(cov(X, X) = var(X)\)
- 公式:\(cov(X, Y) = cov(Y, X)\)
- 公式:\(cov(aX, bY) = ab cov(X, Y)\)
- 相关性:[-1,1]:\(\eta = \frac{cov(X, Y)}{\sqrt{var(X).var(Y)}}\)
- 标准差描述变量在整体变化的过程中偏离均值的程度,协方差除以标准差,也就是把协方差中变量变化幅度对协方差的影响去除掉,这样协方差就标准化了。.
- 协方差与相关系数的关系
2.3、贝叶斯定理
- 计算在一个变量给定的条件下另一个变量发生的概率。 \(P(x|y) = \frac{P(y|x)P(x)}{P(y)}\)
- 在具体的分类中是将在给定特征下求标签的概率转化为给标签求特征的概率
2.4、极大似然估计
- 通过利用已知样本的信息,反推出最大概率导致这些样本结果出现的参数值
- 使用的前提是独立同分布 \(\hat \theta = argmax_{\theta} ln l(\theta) = argmax_{\theta} \sum_{i=1}^N ln P(x_i | \theta)\)
- 参考
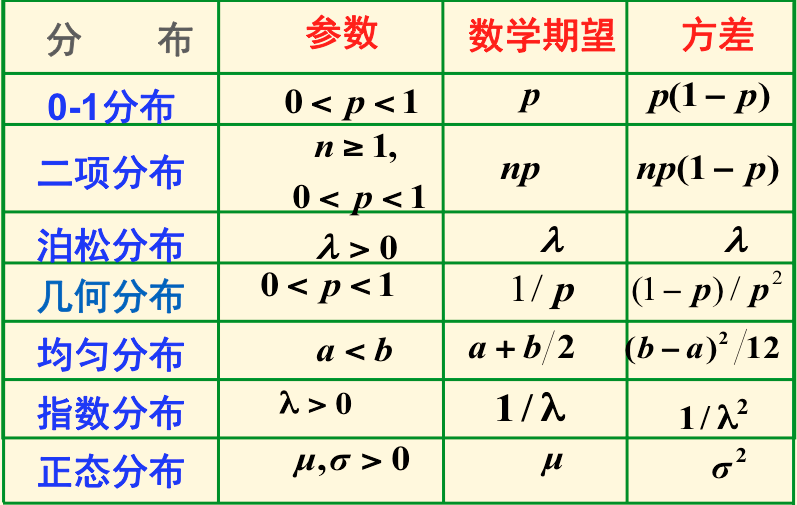
2.5、常见概率分布
2.5.1、离散随机变量
- 伯努利分布:掷硬币,正面概率为p,若为正记1,否为0.\(p(x)=\left\{\begin{array}{ll}{p} & {\text { if } p=1} \\ {1-p} & {\text { if } p=0}\end{array}\right.\)
- 二项分布:掷硬币,正面概率为p,投掷n次为正记做:\(p(x)=\left(\begin{array}{l}{n} \\ {x}\end{array}\right) p^{x}(1-p)^{n-x}\)
- 几何分布:在伯努利实验中,记事件A发生概率为p,试验进行到事件A出现为止,此时所进行的试验测试为X:\(p(X=k) = (1-p)^{k-1}p\)
- 泊松分布:描述单位时间内随机事件发生的次数。\(p(x)=e^{-\lambda} \frac{\lambda^{x}}{x !}\)
- 参考
- k表示k次
- \(\lambda\)表示均值
2.5.2、连续随机变量
- 均匀分布:在a,b间每个点概率密度相同的分布:\(f(x)=\left\{\begin{array}{ll}{\frac{1}{b-a}} & {\text { if } a \leq x \leq b} \\ {0} & {\text { otherwise }}\end{array}\right.\)
- 指数分布:\(\lambda >0\),\(f(x)=\left\{\begin{array}{ll}{\lambda e^{-\lambda x}} & {\text { if } x \geq 0} \\ {0} & {\text { otherwise }}\end{array}\right.\)
- 正态分布:\(f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}}\)
- 一些特性:
2.6、MLE、MAP
2.6.1、MLE最大似然估计
- 贝叶斯公式将后验概率转化为先验概率与似然函数
- MLE本质就是求出似然函数取值最大的时候的参数: \(\hat{\theta}_{M L}=\operatorname{argmax}_{\theta} L(\theta | X)=\operatorname{argmax}_{\theta} \sum_{x \in X} \log p(x | \theta)\)
- 由于似然函数为连乘,所以加上log简化运算
2.6.2、MAP最大后验估计
- 与最大似然估计的区别在于考虑了先验概率
- 计算的是贝叶斯计算后的整个后验概率: \(\begin{aligned} \hat{\theta}_{M A P} &=\operatorname{argmax}_{\theta} \frac{p(X | \theta) p(\theta)}{p(X)} \\ &=\operatorname{argmax}_{\theta} p(X | \theta) p(\theta) \\ &=\operatorname{argmax}_{\theta}\{L(\theta | X)+\log p(\theta)\} \\ &=\operatorname{argmax}_{\theta}\left\{\sum_{x \in X} \log p(x | \theta)+\log p(\theta)\right\} \end{aligned}\)
- 从公式中也可以看出,相较于最大似然估计,加上了先验分布概率的对数
2.7、累积概率密度概率质量函数
随机变量的概率度量
2.7.1、累积分布函数
- \(F(x) = P(x<= x)\),取值为[0,1]
- 性质 \(0 \leq F_{X}(x)\leq 1 \\ \lim _{x \rightarrow-\infty} F_{X}(x)=0 \\ \lim _{x \rightarrow\infty} F_{X}(x)=1 \\ x \leq y \Longrightarrow F_{X}(x)\leq F_{X}(y)\)
- 分布函数
2.7.2、概率质量函数
- 离散变量在各个取值的概率
- 公式:\(P(x) = P(X=x)\)
- 性质: \(0 \leq p_{X}(x)\leq 1 \\ \sum_{x \in Val} p_{X}(x)=1\)
- 类比物理中的质量和密度
2.7.3、概率密度函数
- 连续的话,累积分布函数可导,将累积分布函数的导数称为概率密度函数\(f_{X}(x) \triangleq \frac{d F_{X}(x)}{d x}\)
- 性质: \(f_X(x)\geq 0 \\ \int_{-\infty}^{\infty} f_{X}(x)=1\)
- 与分布函数互为微积分
2.8 链式法则:
\(\begin{aligned} f\left(x_{1}, x_{2}, \ldots, x_{n}\right) &=f\left(x_{n} | x_{1}, x_{2} \ldots, x_{n-1}\right) f\left(x_{1}, x_{2} \ldots, x_{n-1}\right) \\ &=f\left(x_{n} | x_{1}, x_{2} \ldots, x_{n-1}\right) f\left(x_{n-1} | x_{1}, x_{2} \ldots, x_{n-2}\right) f\left(x_{1}, x_{2} \ldots, x_{n-2}\right) \\ &=\cdots=f\left(x_{1}\right) \prod_{i=2}^{n} f\left(x_{i} | x_{1}, \ldots, x_{i-1}\right) \end{aligned}\)
- 贝叶斯中多变量应用
三、线代
3.1、 矩阵乘法
3.1.1、向量-向量乘法
- 内积:结果为实数 \(x^{T} y \in \mathbb{R}=\left[\begin{array}{llll}{x_{1}} & {x_{2}} & {\cdots} & {x_{n}}\end{array}\right]\left[\begin{array}{c}{y_{1}} \\ {y_{2}} \\ {\vdots} \\ {y_{n}}\end{array}\right]=\sum_{i=1}^{n} x_{i} y_{i}\)
- 外积:结果为矩阵 \(x y^{T} \in \mathbb{R}^{m \times n}=\left[\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{m}}\end{array}\right]\left[\begin{array}{llll}{y_{1}} & {y_{2}} & {\cdots} & {y_{n}}\end{array}\right]=\left[\begin{array}{cccc}{x_{1} y_{1}} & {x_{1} y_{2}} & {\cdots} & {x_{1} y_{n}} \\ {x_{2} y_{1}} & {x_{2} y_{2}} & {\cdots} & {x_{2} y_{n}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {x_{m} y_{1}} & {x_{m} y_{2}} & {\cdots} & {x_{m} y_{n}}\end{array}\right]\)
- 3.4节点积叉乘的区别
3.1.2、矩阵-向量乘法
- 向量与矩阵的每一列进行点积组成新的向量。意义矩阵把向量映射到列向量子空间中的一个向量上
3.1.3、矩阵-矩阵乘法
- 矩阵乘法
- 矩阵乘法交换律: \((AB)C = A(BC)\)
- 矩阵乘法分配律: \(A(B + C) = AB + AC\)
3.2 运算和属性
- 单位矩阵:是一个对焦元素为1,其他元素都为0的方阵
- 性质1:\(AI = A = IA\)
- 对角矩阵,除过对角线元素,全为0
- 转置:翻转行列
- 性质1:\((A^T)^T = A\)
- 性质2:\((AB)^T = B^TA^T\)
- 性质3:\((A+B)^T = A^T + B^T\)
-
对称矩阵:若A的转置和A相等,则A为对称矩阵,\(A+A^T\)是对称的。
-
矩阵的迹(tr(A)):对角线元素之和
-
范数:向量长度的度量,基于欧几里得距离:\(\|x\|_{2}=\sqrt{\sum_{i=1}^{n} x_{i}^{2}}\)
-
线性相关性:一组向量,如果没有向量可以表示为其余向量的线性组合,则称该向量是线性无关的,反之为线性相关。
-
秩:列秩等于行秩,用rank(A)表示。
- 方阵的逆:\(A^{-1}A = I = AA^{-1}\),可逆又称为非奇异。
- 性质1:\((A^{-1})^{-1} = A\)
- 性质2:\((AB)^{-1} = B^{-1}A^{-1}\)
- 总之3:\((A^{-1})^{T} =(A^{T})^{-1}\)
-
正交矩阵:\(X^TY=0\)则正交。
-
行列式:一个方阵的行列式函数det,可以表示为|A|或者detA。 \(\begin{aligned}|A| &=\sum_{i=1}^{n}(-1)^{i+j} a_{i j}\left|A_{\backslash i, \backslash j}\right| \quad(\text { for any } j \in 1, \ldots, n) \\ &=\sum_{j=1}^{n}(-1)^{i+j} a_{i j}\left|A_{\backslash i, \backslash j}\right| \quad(\text { for any } i \in 1, \ldots, n) \end{aligned}\)
-
正定矩阵:特征值大于0,一定是满秩的,也就是可逆的。
-
特征值特征向量:\(Ax=\lambda x,x \ne 0\),称其分别为A的特征向量和特征值
- 特征值:运动的速度、拉伸的长度
- 特征向量:运动的方向、拉伸的方向
3.3、矩阵微积分
定义: \(\nabla_{A} f(A) \in \mathbb{R}^{m \times n}=\left[\begin{array}{cccc}{\frac{\partial f(A)}{\partial A_{11}}} & {\frac{\partial f(A)}{\partial A_{12}}} & {\cdots} & {\frac{\partial f(A)}{\partial A_{1n}}} \\ {\frac{\partial f(A)}{\partial A_{21}}} & {\frac{\partial f(A)}{\partial A_{22}}} & {\cdots} & {\frac{\partial f(A)}{\partial A_{2 n}}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial f(A)}{\partial A_{m 1}}} & {\frac{\partial f(A)}{\partial A_{m 2}}} & {\cdots} & {\frac{\partial f(A)}{\partial A_{m n}}}\end{array}\right]\) 相当于是偏导数对多变量函数的自然延伸。
Hessian矩阵: \(\nabla_{x}^{2} f(x) \in \mathbb{R}^{n \times n}=\left[\begin{array}{cccc}{\frac{\partial^{2} f(x)}{\partial x_{1}^{2}}} & {\frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{n}}} \\ {\frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{1}}} & {\frac{\partial^{2} f(x)}{\partial x_{2}^{2}}} & {\cdots} & {\frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{n}}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial^{2} f(x)}{\partial x_{n} \partial x_{1}}} & {\frac{\partial^{2} f(x)}{\partial x_{n} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f(x)}{\partial x_{n}^{2}}}\end{array}\right]\) Hessian是一个对称矩阵
- $\nabla_{x} b^{T} x=b$。
- $\nabla_{x} x^{T} A x=2 A x$,(如果$A$是对称阵)
- $\nabla_{x}^2 x^{T} A x=2 A $, (如果$A$是对称阵)
3.4 点乘、叉乘
- 点乘(点积,内积):各个对应元素做乘法,结果为标量:\(a \bullet b\),表示模长相乘再乘上余弦夹角
- 叉乘(向量积、外积、叉积):结果为向量,并且是春之语所构成平面的法向量.\(a \times b=\left|\begin{array}{lll} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \end{array}\right|=\left(y_{1} z_{2}-y_{2} z_{1}\right) i-\left(x_{1} z_{2}-x_{2} z_{1}\right) j+\left(x_{1} y_{2}-x_{2} y_{1}\right) k\)