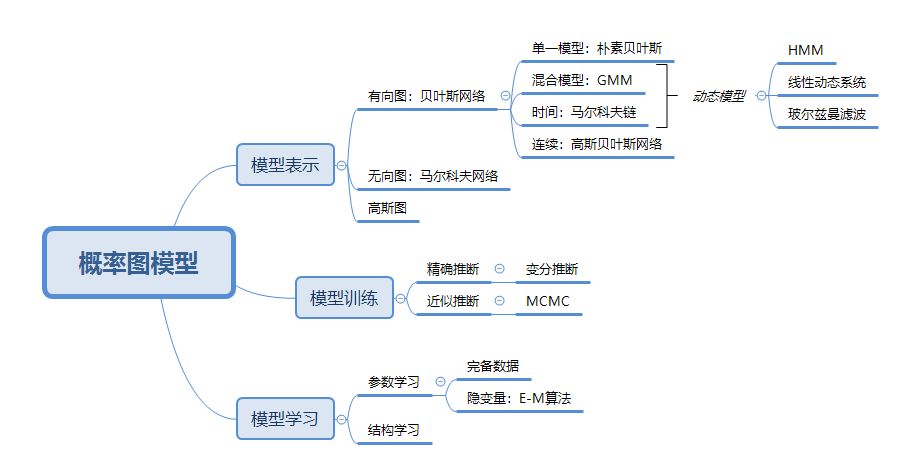
基本概念
- 概率图模型用图的形式表现出上图中的各种假设。节点表示随机变量，边表示条件概率
- 概率图模型有以下三大问题：
- 在图中引入概率模型，图的概念和数据结构中的图概念一样
- 同时概率图模型一般处理的是高维随机变量，其中主要关心的是边缘概率\(P(x_i)\)和条件概率\(P(x_j,given,x_i)\)
- 一些规则： \(加法：P(x_1) = \int P(x_1,x_2)dx_2\\ 乘法：P(x_1,x_2) = P(x_1)P(x_2|x_1)=P(x_2)P(x_1|x_2)\\ 链式：P(x_1,x_2,...,x_p)=P(x_1)\prod_{i=2}^n P(x_i|x_{i-1}-x_{n-1})\\ 贝叶斯：P(x_1|x_2)=\frac{P(x_2|x_1)P(x_1)}{P(x_2)}\)
- 通过概率图模型可以方便的刻画随机变量间不同的条件独立关系。
贝叶斯网络
- 在联合概率分布和随机变量之间的关系，可以通过拓扑排序获得有向图，而通过有向图可以很快的得到联合概率的因子分解。 \(P(x_1,x_2,...,x_p) = \prod_{i=1}^p P(x_i|x_{parent(i)})\)
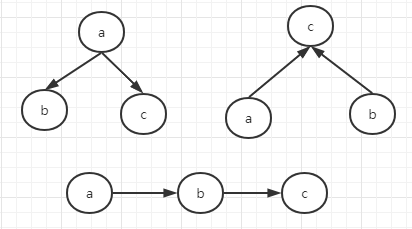
- 下图为三种典型的结构：
- 三种结构的联合概率分布可以写作 \(第一种：P(a,b,c) = P(a)P(b|a)P(c|a)=p(a)P(b|a)P(c|a,b)->给定a，b与c相互独立\\ 第二种：P(a,b,c) = p(a)P(b)P(c|a,b)=p(a)P(b|a)P(c|a,b)->a，b相互独立，给定c则不独立\\ 第三种：P(a,b,c) = P(a)P(b|a)P(c|b)=p(a)P(b|a)P(c|a,b)->给定b，a与c相互\) 通过连式法则证明概率图模型表示了原始的独立假设。
- 有向图的条件独立性：D划分，如下图
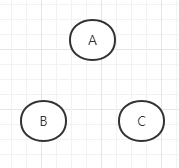A和B之间的关系如果是第一种或者第三种则中间节点必须存在C中，如果有第二种关系，则必须在C节点之外。
马尔科夫网络
- 无向图没有类似有向图的局部不同结构，在马尔科夫网络中，也可以进行D划分。直接将条件独立几何划分为三个集合，对应的就是全局马尔科夫性。对应上面的D划分就是A与B之间的路径中的节点最少有一个在C中。
- 成对马尔科夫：a节点与b节点在给定除过a，b节点外的其他节点的情况下，a，b相互独立（a,b之间没有直接联系）
- 局部马尔科夫：当前点在给定其邻居节点的情况下，其与除过自己和邻居节点外的其他节点相互独立
- 为了引入因子分解，需要最大团，最大团指的是：图中节点的集合，集合中的节点之间相互都是连接的叫做团，如果不能再添加节点，那么叫最大团。
- 基于此，对x进行联合概率因子分解，假设K个团，Z对应所有可能取值的求和 \(P(x) = \frac{1}{Z}\prod_{i=1}^K \psi (x_{ci})\\ Z = \sum_{x\in X}\prod_{i=1}^K \psi (x_{ci})\) 其中\(\psi (x_{ci})\)为势函数，必须是正数，可以记\(\psi (x_{ci}) = exp(-E(x_{ci}))\)
- 基于最大团的分解符合条件独立性，基于\(Hammesley-Clifford\)定理可以证明。
道德图
- 将有向图转化为无向图： \(第一种：p(a,b,c)=P(b)P(a|b)P(c|b)=\psi (a,b)\psi (b,c)\\ 第二种：P(a,b,c)=P(a)P(b|a)P(c|b)=\psi (a,b)\psi (b,c)\\ 第三种：P(a,b,c)=P(a)P(c)P(b|a,c)=\psi (a,b,c),于是a，c之间添加了线\)
- 总结上面的公式可以概括为：
- 将每个节点的父节点两两连接
- 将有向边替换为无向边
因子图
注：对于一个有向图，可以通过引入环的方式，可以将其转换为无向图（Tree-like graph），这个图就叫做道德图。但是我们上面的 BP 算法只对无环图有效，通过因子图可以变为无环图。
-
考了一个无向图：
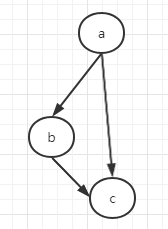将其转化为：
-
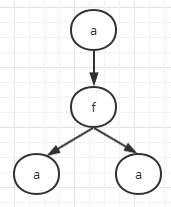
其中 \(f=f(a,b,c)\)。因子图不是唯一的，这是由于因式分解本身就对应一个特殊的因子图，将因式分解：\(p(x)=\prod\limits_{s}f_s(x_s)\) 可以进一步分解得到因子图。
推断
- 推断的目的在于：
- 求边缘概率
- 条件概率
- MAP方式求解参数
- 分类
- 精确推断：
- variable Elimination VE
- Belief progagation,从VE发展而来
- Junction Tree，上面两种在树结构中应用，当前方法在图结构应用
- 近似推断：
- Loop Belief progagation，针对有环图
- MCMC
- Variational Inference
- 精确推断：
变量消除VE
- 变量消除就是在求解概率分布的时候，将相关的条件概率归类先进行求和，，从而一步步消除变量，例如在马尔科夫链中： \(p(d)=\sum_{a, b, c} p(a, b, c, d)=\sum_{c} p(d | c) \sum_{b} p(c | b) \sum_{a} p(b | a) p(a)\)
- 缺点：
- 计算没有存储，计算每个节点都要从头开始计算
- 消除的最优词序是一个np-hard问题
