为什么需要做词向量
不同于语音信号和图像数据，其都有已经定义好的向量空间，天然的就有一组向量或者矩阵来表示一张图片或者一组语音信号的意义。但是对于语言文字来说，不存在一组基组成空间，来表示每一个字或者单词，所以需要我们自己找出来或者说自己定义一组基来对字或者词语进行向量化，用一组向量或者矩阵来对字词句进行表示。
如果不进行向量化的表示，则对于词或者字来说只是一堆离散的标识，没有办法来说明其之间的关系，同时也无法被ML或者DL所操作，所以需要对其进行向量化或者说是数字化的操作。
当然对于早期机器学习中，对文本也会有进行人工特征的提取，从而人为的定义好或者通过某些方法比如tfidf、bm25等来定义特征表示一个字或者词句子等。这些方法得到的特征好处是可解释性强，但是得到的语义过于片面，同时也很难表示复杂的语义信息。
独热编码
算是比较简单也容易想到的一种编码。比如我们所有语料组成的词库有100个词，则每个词都可以表示为一个100维的向量。比如第一个词的编码就是第一位为1，剩下的都是0，同理可以得到其他词的编码。但是现实中词库中词的数量可以达到数十万上百万，如果采用这一种方法的话很容易就会维度爆炸，无法计算。同时如果采用独热编码的话，词语与词语之间全部正交，没有关系，相当于找到了一组基来表示词语，但是所有的词语都在坐标轴上，两两垂直。这样没有办法衡量词语之间的关系。
神经网络语言模型
语言模型
对于一个句子\(w_1,...,w_k\)，语言模型可以计算这个句子序列的概率，依据条件概率，将联合概率分解：\(P(w) = \prod_[k=1]^K P(w_k|w_{k-1},.....,w_1)\)。但是实际情况下，语言模型很难考虑特别长的历史，因此，我们会限定当前次的概率依赖于之前的N-1个词，这也就是\(N-gram\)模型。用公式表示就是\(P(w) = \prod_[k=1]^K P(w_k|w_{k-1},.....,w_{k-N+1})\),实际的应用中取值2-5.语言模型的评价标准一般是困惑度Perplexity。
\[\begin{aligned} H &=-\lim _{K \rightarrow \infty} \frac{1}{K} \log _{2} P\left(w_{1}, \ldots, w_{K}\right) \\ & \approx \frac{1}{K} \sum_{k=1}^{K} \log _{2}\left(P\left(w_{k} \mid w_{k-1}, \ldots, w_{k-N+1}\right)\right) \end{aligned}\]N-gram语言模型通常通过最大似然方法估计参数，比如\(C(w_{k-2}w_{k-1}w_k)\)表示三个词连续出现的次数，\(C(w_{k-2}w_{k-1})\)表示两个词连续出现的次数，则：\(P\left(w_{k} \mid w_{k-1} w_{k-2}\right)=\frac{C\left(w_{k-2} w_{k-1} w_{k}\right)}{C\left(w_{k-2} w_{k-1}\right)}\)
但是上面的方法会出现问题，比如词库稀缺，数据的稀疏性就会非常严重，如果某几个词没有连续出现在语料库中，则概率会为0.但是语料库总会给你没有出现的数据并不代表其是不合理的。通常的处理方法有打折或者回退等平滑方法来改进。
问题：N-gram中的N不能太大，否则需要存储的N-gram过多（因为会有回退折扣等改进方法的影响，所以会需要存储更多的N-gram）。泛化能力差，由于是基于词的共现，所以如果没有出现的词概率会很小，但是相同性质的词应该在同一个语境中概率类似。
神经网络语言模型
神经网络如下图所示：
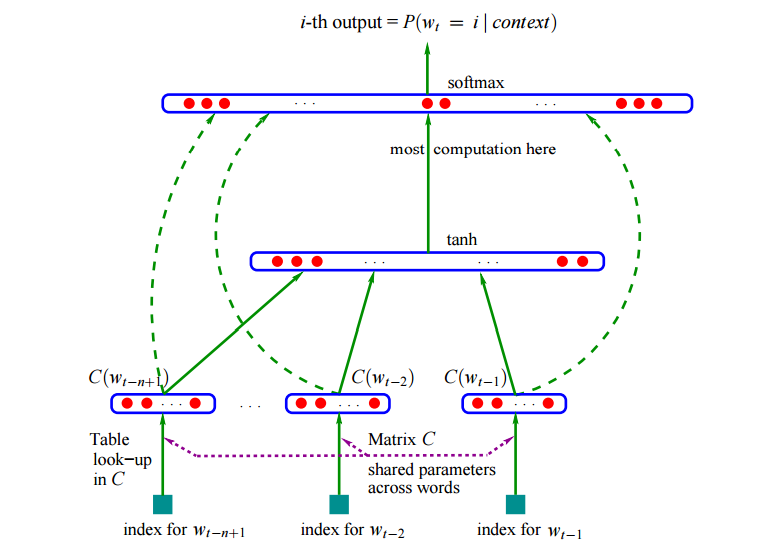图解：借助语言模型，需要预测的词作为输出，词前面的数据作为输入。比如机器学习，需要预测习，输入机器学，预测输出为习。如图所示，输入先one-hot然后与随机生成的共享词矩阵相乘得到输入的向量矩阵，然后经过激活函数层进行计算，最后经过softmax进行计算得到预测词的结果。
word2vec
获取词向量的方法有很多，可以通过语言模型，或者其他的任务，但是词向量基本都是其副产品，获取词向量的代价太大，\(Mikolov\)等提出word2vec直接用于训练词向量。速度快，专门用于生成词向量。
word2vec的基本思想：词的上下文想类似，则词的意思类似，也就是说词的意思可以通过上下文来给出。其有两种方法一种是CBOW一种是Skip-gram。CBOW是通过给定上下文来预测当前词，Skip-gram是给定当前词来预测CBOW。
CBOW
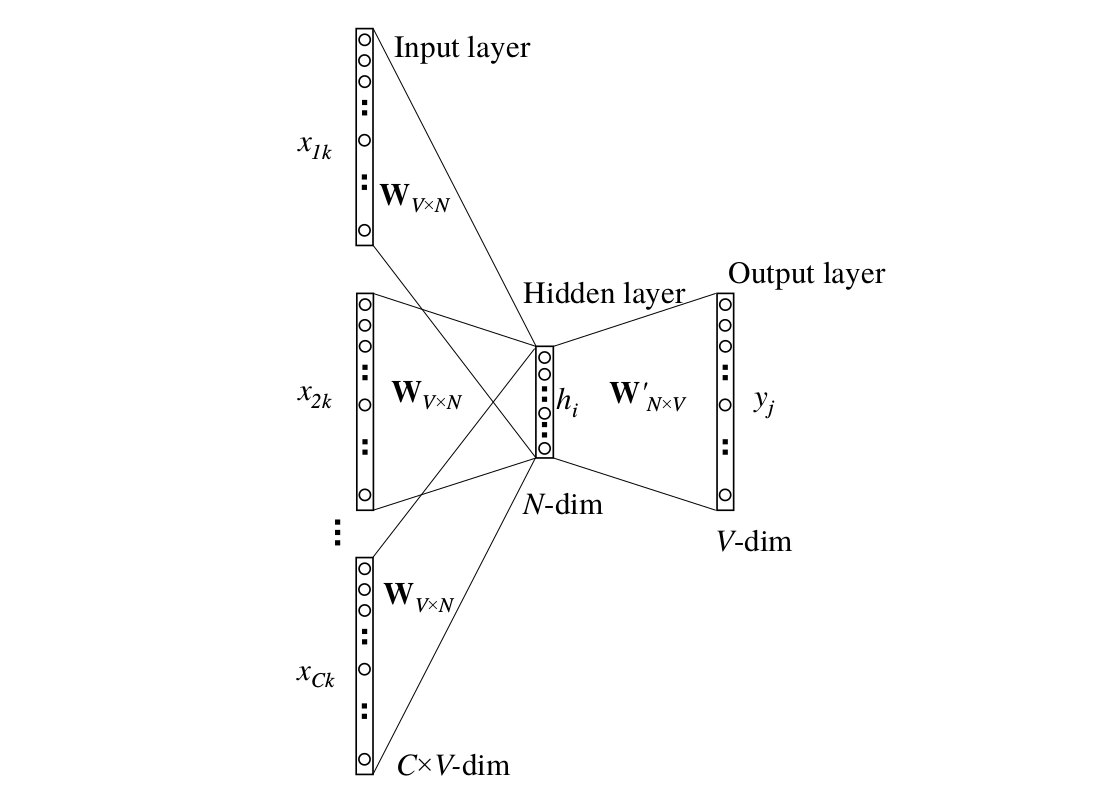
Skip-gram
计算与CBOW类似，基于中心词预测上下文，也就是基于中心词预测上下文词的个数次。计算的loss是预测多次后的loss的均值。 参考
计算效率
不管是CBOW还是Skip-gram在计算反向求导参数更新的时候，在输出层到隐藏层的传播中需要更新所有的上下文词向量，在实际应用中，上下文词的个数会跟多，这样计算效率就会变得很低。 优化方法:层次softmax, 负采样
Glove
- 目标：对词语进行向量的表示，使得表示出来的向量能尽可能的表达词语蕴含的信息
- 输入：语料库
- 输出：词向量
- 方法：首先基于语料库构建词的共现矩阵，然后基于共现矩阵和Glove模型学习词向量
共现矩阵
设共现矩阵为X，其元素为\(X_{ij}\)
\(X_{ij}\)的意义为：在整个语料库中，单词i和单词j共同出现在一个窗口的次数
例如：‘i love you but you love him i am sad’。这个语料库有一个句子，涉及7个单词，如果我们采用窗口宽度为5的统计窗口，那么就有以下窗口内容：
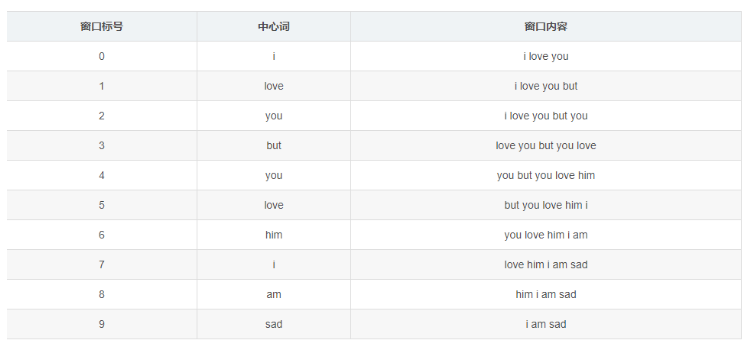
窗口0,1,8,9因为中心词的问题长度小于5.以窗口为5为例说明构造共现矩阵：
中心词为love，语境词为but、you、him、i，则执行：\(X_{love,but} + = 1, X_{love,you} += 1, X_{love,him} += 1, X_{love, i} += 1\)
使得窗口将整个语料遍历一遍，即可得到共现矩阵X。
模型公式
代价函数为： \(J=\sum_{i, j}^{N} f\left(X_{i, j}\right)\left(v_{i}^{T} v_{j}+b_{i}+b_{j}-\log \left(X_{i, j}\right)\right)^{2}\) \(v_i, v_j\)是单词i和单词j的词向量，\(b_i, b_j\)是两个变量为偏差，f为权重函数，N为词汇表大小（共现矩阵维度为N*N）
推导过程
定义\(X_i = \sum_{j=1}^NX_{i,j}\)为矩阵单词i哪一行的和；\(P_{i,k} = \frac{X_{i,k}}{X_i}\)条件概率，表示单词K出现在单词i语境中的概率；\(ratio_{i,j,k} = \frac{P_{i,k}}{P_{j,k}}\)两个条件概率的比率，也就是单词K出现在单词i语境的概率比上单词K出现在单词j语境中概率
\(ratio_{i,j,k} = \frac{P_{i,k}}{P_{j,k}}\)这个指标是有规律的，如下表：
思想：假设我们已经得到词向量\(v_i, v_j, v_k\)通过某种函数计算\(ratio_{i,j,k}\)，能够同样得到这样的规律，就意味我们的词向量和共现矩阵具有一致性，也就说明我们的词向量中蕴含了共现矩阵中所蕴含的信息。
设用\(v_i, v_j, v_k\)计算\(ratio_{i,j,k}\)的函数为\(g(v_i, v_j, v_k)\)，那么应该有： \(\frac {P_{i,k}}{P_{j,k}} = ratio_{i,j,k} = g(v_i, v_j, v_k)\) 也就是说： \(\frac {P_{i,k}}{P_{j,k}} = g(v_i, v_j, v_k)\) 即需要两者的信息足够的接近，自然的一种想法是： \(J=\sum_{i, j, k}^{N}\left(\frac{P_{i, k}}{P_{j, k}}-g\left(v_{i}, v_{j}, v_{k}\right)\right)^{2}\) 但是细看，模型中含有三个单词，就意味着要在NNN的复杂度上计算，太复杂。
作者假设：
- 要考虑单词i和单词j之间的关系，哪\(g(v_i, v_j, v_k)\)种大概要有这么一项\(v_i - v_j\)。在线性空间中考察两个向量的相似性，不失线性的考察，那么\(v_i - v_j\)大概是一个合理的选择
- \(ratio_{i,j,k}\)是一个标量，那么\(g(v_i, v_j, v_k)\)最后应该也是标量，那么内积应该是合理的选择，于是就有\((v_i - v_j)^Tv_k\)
- 再给\((v_i - v_j)^Tv_k\)加上exp，得到最终的\(g(v_i, v_j, v_k) = exp((v_i - v_j)^Tv_k)\)
最终，我们的目标是希望以下公式尽可能的成立： \(\frac {P_{i,k}}{P_{j,k}} = g(v_i, v_j, v_k)\\ \frac {P_{i,k}}{P_{j,k}} = exp((v_i - v_j)^Tv_k)\\ \frac {P_{i,k}}{P_{j,k}} = exp(v_i^Tv_k - v_j^Tv_k)\\ \frac {P_{i,k}}{P_{j,k}} = \frac{exp(v_i^Tv_k)}{exp(v_j^Tv_k)}\) 然后就发现找到了简化的方法，只需要让上面的分子分母对应相等就可以了，也就是： \(P_{i,k} = exp(v_i^Tv_k)\\ P_{j,k} = exp(v_j^Tv_k)\) 然而分子分母形式相同，就可以统一考虑： \(P_{i,j} = exp(v_i^Tv_j)\\ so: P_{i,j} = exp(v_i^Tv_j)\\ log(P_{i,j}) = v_i^Tv_j\) 则代价函数简化为： \(J = \sum_{i,j}^N(log(P_{i,j}) - v_i^Tv_j)^2\) 现在只需要N*N的复杂度就可以计算了，仔细查看： \(Log(P_{i,j}) = v_i^Tv_j\\ Log(P_{j,i}) = v_j^Tv_i\) 左边对应不相等但是右边对应相等，数学上出现了问题。
将代价函数展开：\(log(P_{i,j}) = v_i^Tv_j\) 即为： \(log(X_{i,j}) - log(X_i) = v_i^Tv_j\\ log(X_{i,j}) = v_i^Tv_j + b_i + b_j\) 即添加一个偏差项\(b_j\)，并将\(log(X_i)\)吸收到偏差\(b_i\)中，则代价函数变为： \(J=\sum_{i, j}^{N}f(x_{i,j})\left(v_{i}^{T} v_{j}+b_{i}+b_{j}-\log \left(X_{i, j}\right)\right)^{2}\) 具体的权重函数f：首先应该是非减的，其次是词频过高的时候，权重不应该过分增大，通过实验的到： \(f(x)=\left\{\begin{array}{ll}{(x / x \max )^{0.75},} & {\text { if } x<x \max } \\ {1,} & {\text { if } x>=x \max }\end{array}\right.\)
两个标量参数称为中心词偏差和背景词偏差
最终的结果是背景词和中心词词向量之和：因为在glove中拟合的是对称的条件概率，即任意词的中心词向量和背景词向量是等价的
fasttext
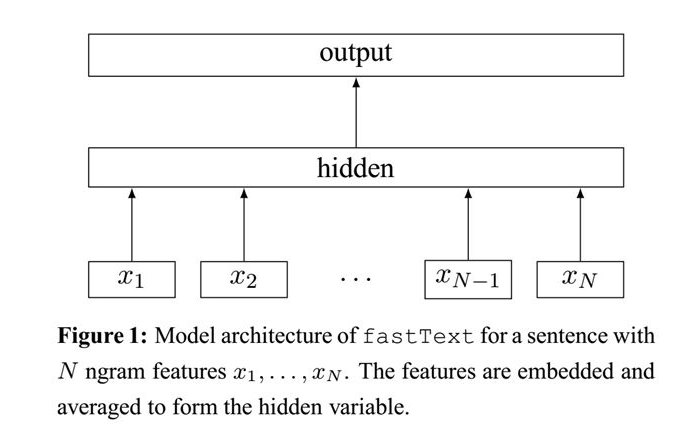
和word2vec中的CBOW类似，在输入做了一定的处理。因为词带模型不考虑词序，所以会出现 一些问题，比如我喜欢她，和她喜欢我，里面的词是一样的，但是意思完全不一样。fasttext再输入的时候不仅输入原始的词序列，同时还加入n-gram信息。可以更加细化的区分信息。同时word2vec也忽略了词内部信息，比如阿里巴巴和阿里有较多的公共字符，我们也知道他们是同义词，但是在word2vec中会将其表示为两个词语，丢失了内部信息。加入n-gram还有好处就是对于出现次数比较少的词效果也有保证，因为n-gram信息是共享的。和CBOW还有一点不同是，CBOW的输出是词语，fasttext的输出是标签，词向量相当于是副产品。
注：fasttext的核心思想，是对输入的词以及相应n-gram向量进行平均，然后使用结果进行softmax多分类。
emlo
上述的方法都是表示的一个静态的词向量，不能很好的应用到一词多意的场景。比如两句话
1
2
听说美国的那个川普总统要在墨西哥边上修个墙
同学你的川普挺带感的
上述的方法不能对川普这个词语很好的mebedding。
下面介绍的elmo就是一个动态词向量的方法：
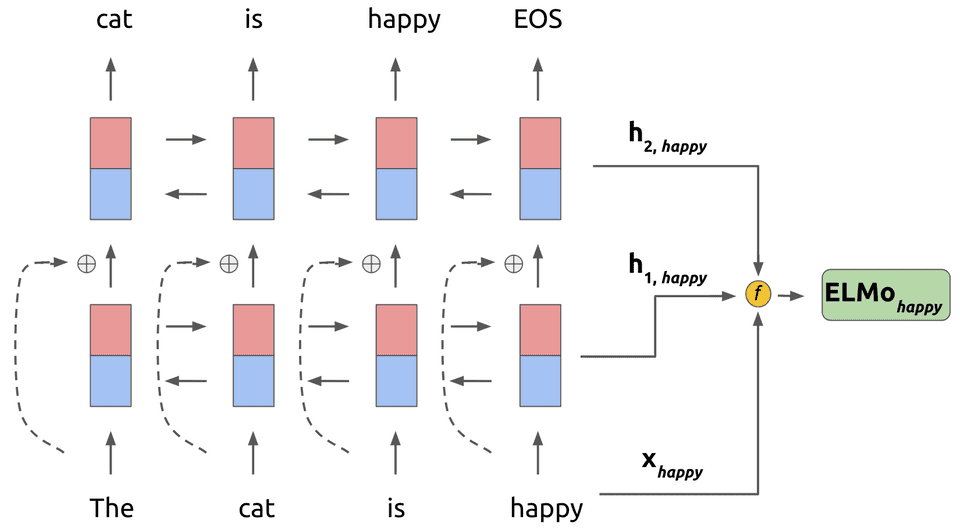整个的模型结构如上图所示：
目标函数为： \(\sum_{k=1}^{N}\left(\log p\left(t_{k} \mid t_{1}, \ldots, t_{k-1} ; \Theta_{x}, \vec{\Theta}_{L S T M}, \Theta_{s}\right)+\log p\left(t_{k} \mid t_{k+1}, \ldots, t_{N} ; \Theta_{x}, \overleftarrow{\Theta}_{L S T M}, \Theta_{s}\right)\right)\)
在预训练阶段，通过L层的两个lstm，一个正向学习，一个反向学习，分别得到各个词的表示。 \(R_{k}=\left\{x_{k}^{L M}, \overrightarrow{h}_{k, j}^{L M}, \overleftarrow{h}_{k, j}^{L M} \mid j=1, \ldots L\right\}\\ 讲输入的embedding作为第0项\\ R_{k}=\left\{h_{k, j}^{L M} \mid j=0, \ldots L\right\}\)
对于一个词，elmo会生成\(2L + 1\)个向量，其中L表示lstm的层数，lstm每一层学习到的知识不相同（底层的偏向于基础语法的学习、深层偏向整体语义的表现），将各层的输出以及原始输入的词向量进行加权综合得到一个符合人物的elmo词向量。比如如果是两层的lstm则每个词会有3个向量表示。
在下游的任务中： \(E L M O_{k}^{t a s k}=E\left(R_{k} ; \Theta^{t a s k}\right)=\gamma^{t a s k} \sum_{j=0}^{L} s_{j}^{t a s k} h_{k, j}^{L M}\\ 其中\gamma 控制向量大小，s论文中表述为softmax-normalized weights，个人理解就是对各个层学习到的向量进行加权，从而可以生成动态的词向量。\)
当然在具体的使用的时候，有时也只是利用最顶层的输出就可以达到不错的效果。同时elmo中lstm换成其他的如cnn、transformer等特征抽取器也可以。但是不同的是其在使用的时候是将句子输入elmo然后结果与下游任务的词向量concat在一起
经测试在短文本的处理中优势比较明显。注意，第一个词和最后一个词也是有上下文的，第一个词和最后一个词的上文和下文都是特使标识。下文和上文都是整个句子。
gpt
gpt1
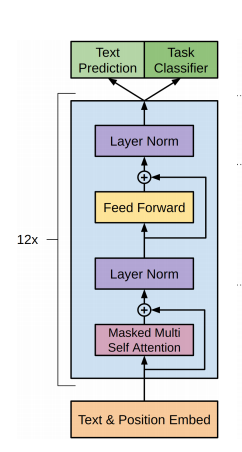
基础是transformer，但是只用了transformer的decoder并且对decoder作为修改，去除了其中的encode-decode-attention。
同时这个模型的过程也是有预训练和有监督的微调两个部分：预训练部分结构如下图所示：
\(使用语言模型最大化如下：\\
L_{1}(U)=\sum_{i} \log P\left(u_{i} \mid u_{i-k}, \ldots, u_{i-1} ; \theta\right)\\
k表示token的个数、\theta 表示语言模型的参数、P表示神经网络模拟的条件概率\\
\begin{array}{c}
h_{0}=U W_{e}+W_{p} \\
h_{l}=\text {transformer_block}\left(h_{l-l}\right) \forall i \in[i, n] \\
P(u)=\operatorname{softmax}\left(h_{n} W_{e}^{T}\right)
\end{array}\\
其中W_e表示词向量矩阵，W_p表示位置向量矩阵\)
微调部分：在最后一层的transformer后加全连接层接softmax构成任务分类层 \(P\left(y \mid x^{1}, \ldots, x^{m}\right)=\operatorname{softmax}\left(h_{l}^{m} W_{y}\right)\\ 预期是输入样本后，预测对的概率最大：\\ L_{2}(\mathcal{C})=\sum_{(x, y)} \log P\left(y \mid x^{1}, \ldots, x^{m}\right)\\ 论文中将两个目标函数结合：L_{3}(\mathcal{C})=L_{2}(\mathcal{C})+\lambda * L_{1}(\mathcal{C})\)
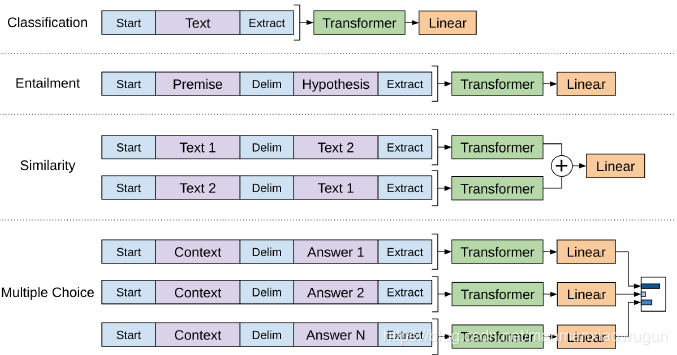如上图中input都是由start开始extract结束。
文本蕴含：输入时前提和假设两个句子，将句子分隔开输入
相似度：由于两个句子的顺序不影响结果，将两种顺序都放入model，结果进行拼接，再到分类器
多项选择：针对每个答案都将问你和答案分别输入
gpt2
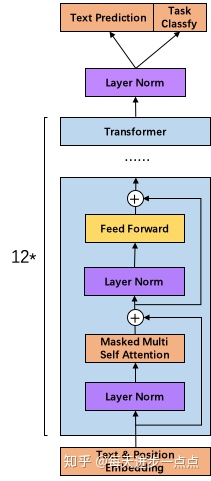
gpt2依然是基于transformer的模型，不过在整体结构上进行了微调：
1
2
3
4
5
去掉了fine-tuning层：不针对任何任务进行调整，自动识别需要完成什么任务
增加数据集：40G文本
增加网络参数：48个block
调整transformer：将LN换到每个子层之前，同时在最后一层的block再加上LN
残差层的参数初始化根据网络深度进行调节
举例说明gpt2：
1
The translation of word Machine Learning in chinese is 机器学习
bert
bert可以说是集大成者，集什么呢，集强特征抽取器、大数据集以及超强算力。当然也有其创新性
1
2
3
4
提出mask language model
使用双向transformer，只是用其encoder
设计两个任务，next sentence以及遮蔽语言模型
简单的预训练方式
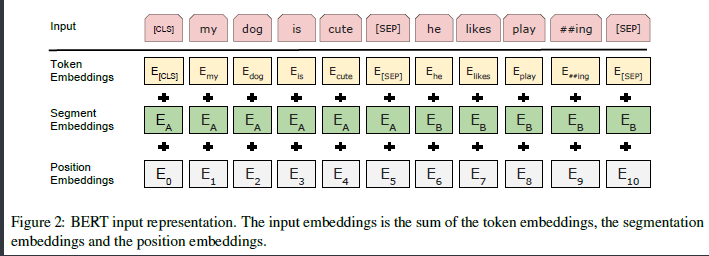[代码注释]
albert
主要为了解决GPU/TPU的内存限制问题。提出以下两种参数减少的技术来降低内存消耗并提高训练速度。
1
2
3
引入SOP，句子间的连贯性，解决bert中提出的下一个句子的预测的无效性
分解词向量：记词表为V，词向量为E，原始的嵌入矩阵为V*E，通常V很大，所以这一层的参数很多并且很稀疏。这里采用嵌入参数的分解，将其分解为两个小的矩阵（与其直接将onehot向量投影到大小为H的隐藏空间中，不如将它们投影到大小为E的低维词向量空间中，然后将其投影到隐藏空间中）。通过这种分解，我们将嵌入参数从O（V×H）减少到O（V×E + E×H）。 当H >> E时，此参数减小非常明显
跨层参数共享：跨层共享所有参数。
注意：虽然albert的参数量减少了，但是预测效率并没有大的变化，因为预测的计算量和bert相比相差无几。
