第一章
-
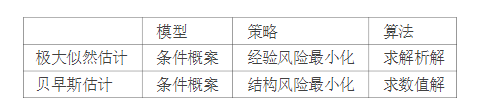
说明伯努利模型的极大似然估计以及贝叶斯估计中的统计学习三要素。伯努利模型是定义在取之为0和1的随机变量上的概率分布。假设观测到伯努利模型n次独立的数据生成结果为，k次为1，这时可以用极大似然估计或者贝叶斯估计来估计结果为1的概率。
答：
设$P(Y=1) = \theta, P(Y=0) = 1 - \theta$。则极大似然估计为：$L(\theta) = \prod_{i=1}^n P(A_i) = \theta ^k (1 - \theta)^{n-k}$。
似然函数的对数为：$ log(L(\theta)) = log(\theta ^k (1 - \theta)^{n-k})= k log(\theta) + (n-k)log(1-\theta)$。
求导并另导数为0:$\partial(\log (L(\theta)) / \partial(\theta)=k /(\theta)-(n-k) /(1-\theta)=0$。得到，$\theta=k/n$ 贝叶斯估计：$P\left(\theta \mid A_{1}, A_{2} \ldots A_{n}\right)=\frac{P\left(A_{1}, A_{2}, \ldots A_{n} \mid \theta\right) \times \pi(\theta)}{P\left(A_{1}, A_{2}, \ldots A_{n}\right)}$ 另：$\theta=\frac{k+(a-1)}{n+(a-1)+(b-1)}$,其中a和b满足beta分布。
则：
-
通过经验风险最小化推导极大似然估计，证明模型是条件概率分布，当损失函数是对数损失函数时，经验风险最小化等价于极大似然估计。
粗糙的解释：最大似然估计：$ max \frac{1}{n} \sum_{i=1}^n log(f(x_i|\theta)$ 也就是经验风险最小化：$min-\frac{1}{n} \sum_{i=1}^n log(f(x_i|\theta)$ 所以模型时伯努利模型，损失函数为对数损失函数，会求解经验风险最小化等价于最大似然估计 精细的解释：模型时条件概率：$f(x) = P(Y|X) = \frac{P(X,Y)}{P(X)}$ 对数损失的定义为：$L(Y, P(Y|X)) = -logP(Y|X)$ 此时经验损失为：$R = \frac{1}{N} \sum_{i=1}^N L(Y_i, f(X_i)) = \frac{1}{N} \sum_{i=1}^N L(Y_i, P(Y_i | X_i))=\frac{1}{N} \sum_{i=1}^N -logP(Y_i|X_i) = -\frac{1}{N} log (\prod_{i=1}^N \frac{P(X_i, Y_i)}{P(X_i)})$
第二章
- 为什么感知机不能表示异或关系。
答：
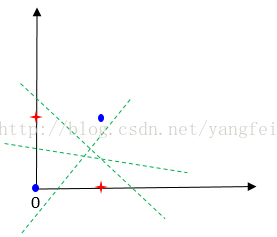感知机所解决的是线性可分问题，但是异或问题如图所示是一种典型的非线性问题，没有办法找到一条直线将其分开。 -
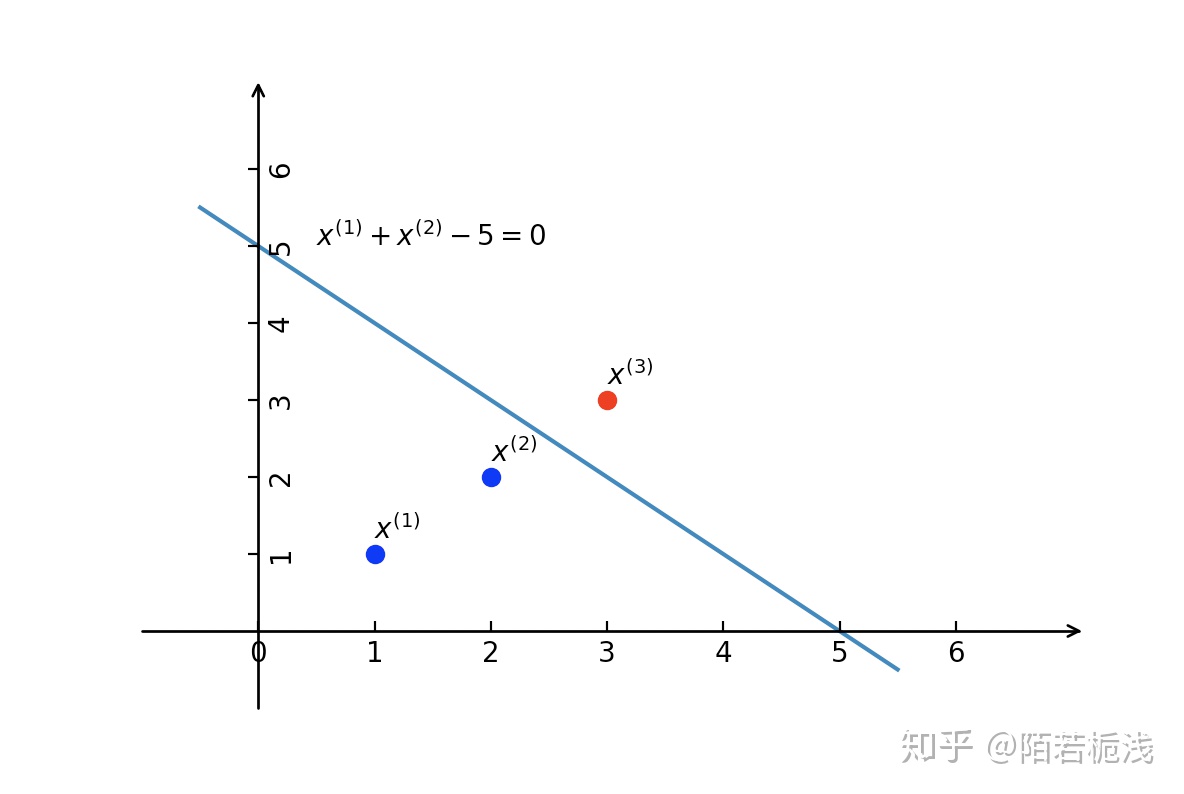
构建从训练数据集求解感知机模型的例子。 答：如图所示，正实例点$x_3 = (3, 3)^T$,负实例点是$x_1 = (1, 1)^T , x_2 = (2, 2)^T$.使用感知机模型$f(x) = sign(w.x +b)$其中$w = (w^1 , w^2)^T , x = (x^1, x^2)^T$
构造最优化问题：$min_{w, b} = -\sum_{x_i \in M} y_i(w.x_i + b)$
按照感知机算法求解w, b，取$\eta = 1$
取初始值$w_0 = 0, b_0 = 0$
对$x_1 = (1, 1)^T, y_3(w_0 . x_3 + b_0) = 0$未被正确分类，更新$w，b, w_1=w_0+y_1 x_1=(-1,-1)^T, b_1=b_0+y_1=-1$
得到线性模型：$w_1 x + b_1 = -x^1 - x^2 - 1$
此时对于$x_3， y_i(w.x_i + b) <= 0$未被正确分类，优化参数：$w_2=w_1+y_3 x_3=(2,2)^T, b_2=b_1+y_3=0$
得到线性模型：$w_2x + b_2 = 2x^1 + 2x^2$
如此往复，直到：$w_{13}=(1,1)^T, b_{13}=-5 w_{13} \cdot x+b_{13}=x^1+x^2-5$
对所有的数据点$y_i(w_{13}x_i + b_{13}) > 0$没有误分类点，损失函数达到最小。
结果分类超平面为：$x^1 + x^2 - 5 = 0$
感知机模型为：$f(x) = sign(x^1 + x^2 - 5)$ - 证明：样本集线性可分的充分必要条件时正实例点集所构成的凸壳与负实例集所构成的凸壳互不相交。 答：详情
