语音识别

CTCloss

"损失函数"

Posted by zwt on September 21, 2020

目的

针对语音识别中字符与因素的对应，手写识别中字符与图片的对应、视频标记中动作的标记等诸如输入与输出对应的问题。 上述场景下（各个输入之间没有明确的界限），正是CTC（Connectionist Temporal Classification）用武之地。CTC是一种让网络自动学会对齐的好方法，十分适合语音识别和书写识别。

基本原理

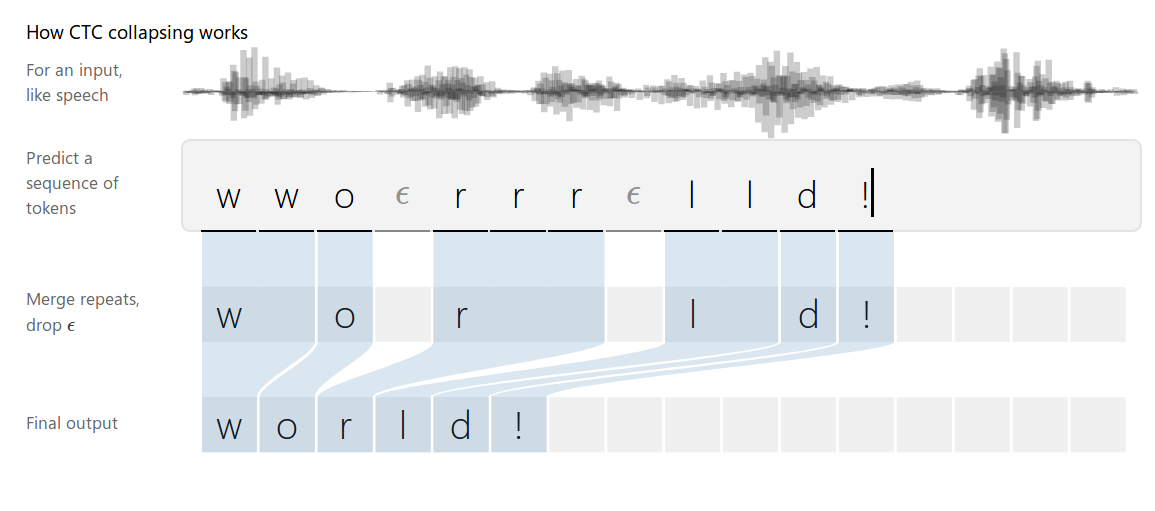如上图所示：ctcloss在字符与字符之间加入特殊的字符$\epsilon$,如果是连续相同的字符之间也要加入特殊符号来做区分。

主要解决的问题

例如对于一个输入序列：$X = [x_1, x_2, x_3,….x_T]$在语音识别中其表示的就是T个帧，每一个帧$x_t$是一个MFCC提取的n维特征，输出序列为：$Y = [y_1, y_2, y_3,….y_U]$ 对于上述的任务来说，很难说将其转化为一般的分类任务，因为：

1
2
3

X和Y都是变长的
X和Y的长度也是变化的，也就是说X和Y的长度之间不存在简单的比例对应关系
训练数据中X和Y很难有对齐的情况

也许有人说可以将其认为是序列标注问题，但是注意，一般的序列标注问题是存在清晰的边界的，输入输出都是逻辑符号，符号之间边界明显，可以很好的建模，同时在前期也被当作分类任务来处理。但是对于语音识别问题，输入的是 语音信号，输入之间没有明显的界限，输入和输出没有办法进行对齐。

CTC的提出就是为了解决这一类问题，对于一个给定的X，CTC可以对所有可能的Y计算P(Y given X)。炸这样就可以计算出相应的某个Y的概率。

CTC给出的是一个较优的路径，是在合理的时间内选择一个可以接受的解。

与softmax不同，softmax需要严格的对齐来计算，ctcloss不需要严格的对齐，通过前向算法对求解的速度进行优化。

详解

对于给定的X，CTC可以计算出所有输出Y的概率，这个计算的关键在于CTC对于输入输出的对齐处理。

对齐

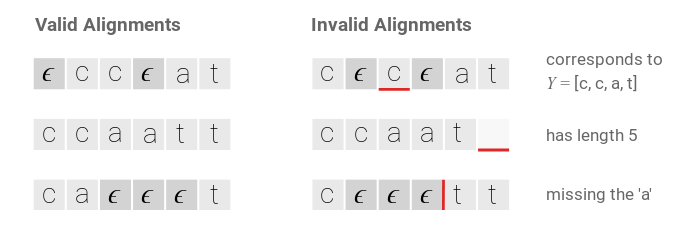
主要解决了两个问题，比如语音识别中的静音，不应该有输出，第二个问题，输出有相同的字符。

损失函数

有了ctc对齐之后，就可以很自然的计算概率P(Y|X)了，计算过程如下： 如上图所示RNN会计算每一个时刻的输出概率分布$p_t(a given X)$，表示t时刻输出字符a的概率。这些概率中有些很小可以忽略，有些对应的输出一样，就加起来。形式化的表示为 $P(Y \mid X)=\sum_{A \in \mathcal{A}{X, Y}} \prod{t=1}^{T} p_{t}\left(a_{t} \mid X\right)$

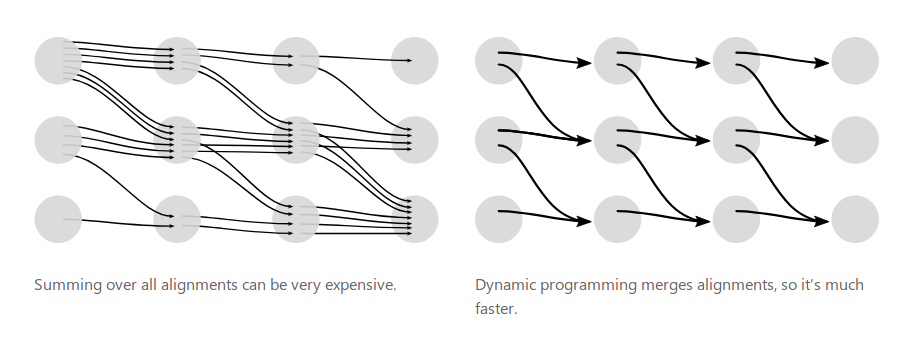
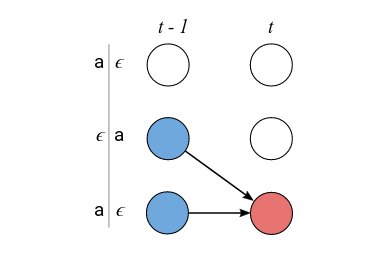
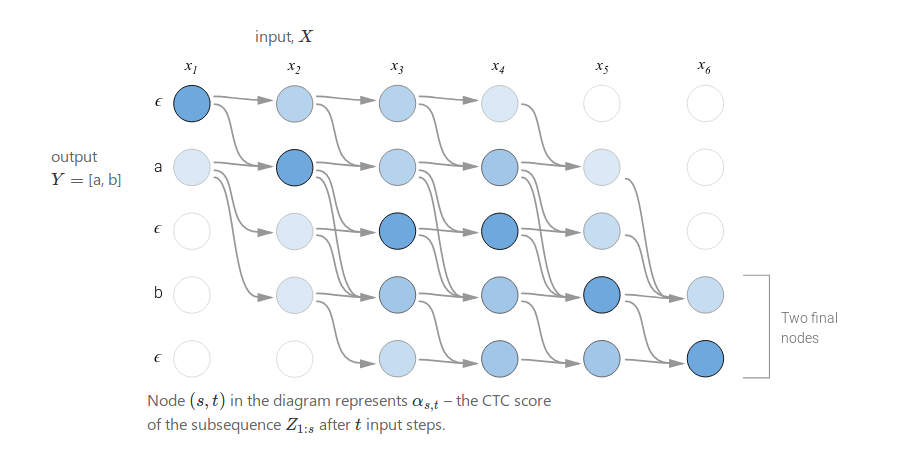
因为在输出y的任意两个字符之间都可以对应空字符，所以我们在y的每一个字符之间都插入空字符得到$Z=[\epsilon , y_1, \epsilon , y_U, \epsilon]$。假设$\alpha_{s,t}$表示输入序列的前s个字符$X_{1:s}$和输出的前t个字符$Z_{1:t}$对齐时所有合法路径的概率和。有了t时刻之前的$\alpha$，我们就可以计算t时刻的$\alpha$，这样我们就可以使用动态规划算法，最后得到T时刻的$\alpha$之后我们就可以得到P(Y|X)。

预测

一种最简单直接的方法：对每一个时刻的输出都选取概率最大的输出，这样就可以得到概率最大的一条路径。$A^{*}=\underset{A}{\operatorname{argmax}} \prod_{t=1}^{T} p_{t}\left(a_{t} \mid X\right)$

可以通过对beam search的改进来完成预测解码： 一般的beam search：

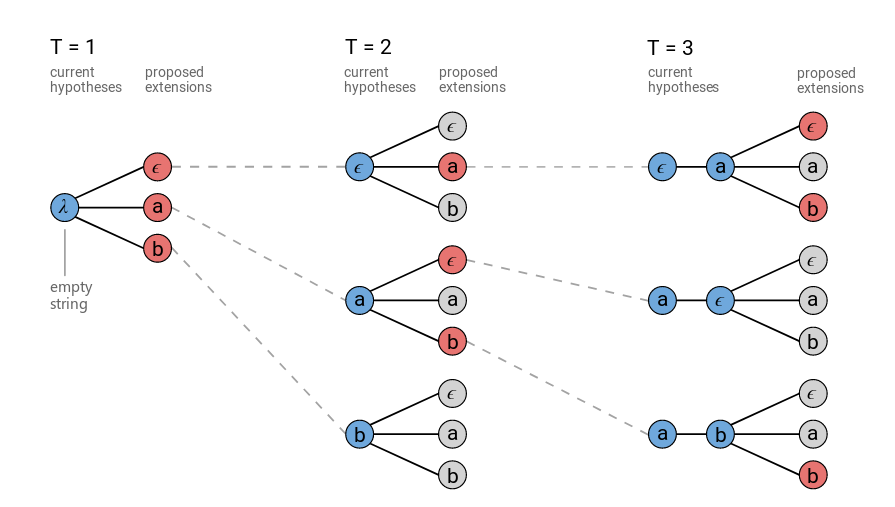
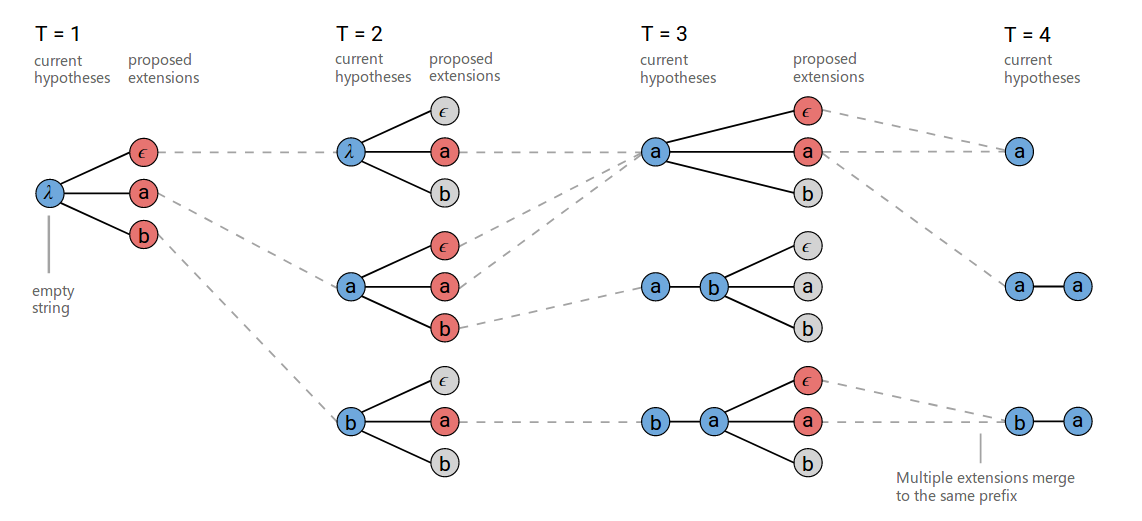
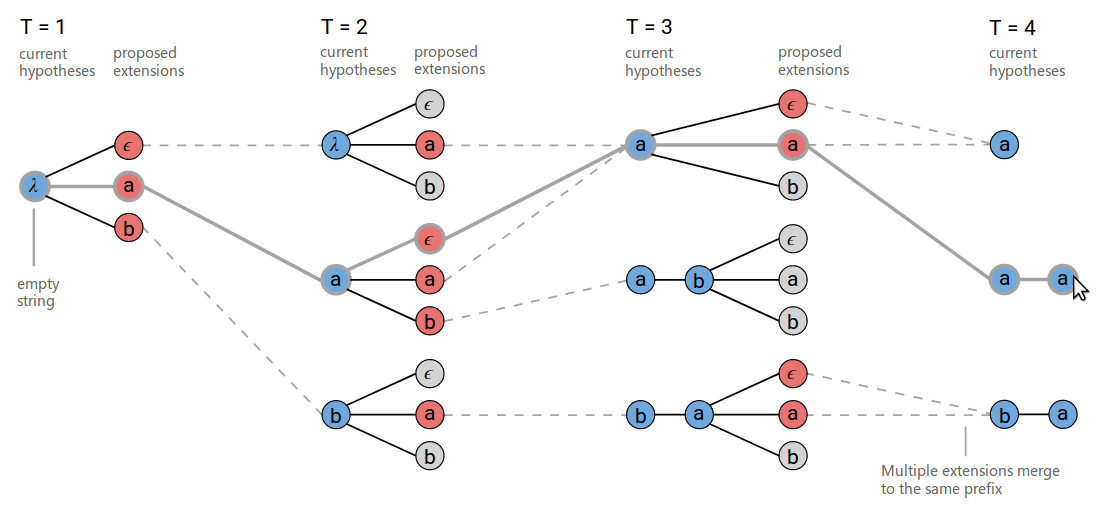
对上述基础的beam search进行改进：如下图所示将输出相同的路径合并，同时去掉空字符，然后所有相同输出的概率累加起来。例如再t为3的时候，下方的$b,a, \epsilon$和$b,a,a$被合并为相同的$b,a$。但是为了防止中间有空字符的情况，需要记录那些最后一个字符为空。

解码

贪心搜索

简单粗暴，在每一个时间点，输出概率最大的标签。

然而输出序列的每一条并不是独立的，一个最终的标签可能对应搜索空间的N条路径，所以概率最大并不能表示最终的标签概率最大，所以只能说是一种近似的解法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

import numpy as np


# 求每一列(即每个时刻)中最大值对应的softmax值
def softmax(logits):
	# 注意这里求e的次方时，次方数减去max_value其实不影响结果，因为最后可以化简成教科书上softmax的定义
	# 次方数加入减max_value是因为e的x次方与x的极限(x趋于无穷)为无穷，很容易溢出，所以为了计算时不溢出，就加入减max_value项
	# 次方数减去max_value后，e的该次方数总是在0到1范围内。
	max_value = np.max(logits, axis=1, keepdims=True)
	exp = np.exp(logits - max_value)
	exp_sum = np.sum(exp, axis=1, keepdims=True)
	dist = exp / exp_sum
	return dist


def remove_blank(labels, blank=0):
	new_labels = []
	# 合并相同的标签
	previous = None
	for l in labels:
		if l != previous:
			new_labels.append(l)
			previous = l
	# 删除blank
	new_labels = [l for l in new_labels if l != blank]

	return new_labels


def insert_blank(labels, blank=0):
	new_labels = [blank]
	for l in labels:
		new_labels += [l, blank]
	return new_labels


def greedy_decode(y, blank=0):
	# 按列取最大值，即每个时刻t上最大值对应的下标
	raw_rs = np.argmax(y, axis=1)
	# 移除blank,值为0的位置表示这个位置是blank
	rs = remove_blank(raw_rs, blank)
	return raw_rs, rs


np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
label_have_blank, label_no_blank = greedy_decode(y_test)
print(label_have_blank)
print(label_no_blank)

集束搜索

由于贪心的方法忽略了一个输出可能对应多个对齐结果的问题，我们可以通过找寻top-n路径来缓解这个问题。

基本思想是，每一步都保留beamsize个节点，到最后一共得到beamsize个路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

import numpy as np


# 求每一列(即每个时刻)中最大值对应的softmax值
def softmax(logits):
	# 注意这里求e的次方时，次方数减去max_value其实不影响结果，因为最后可以化简成教科书上softmax的定义
	# 次方数加入减max_value是因为e的x次方与x的极限(x趋于无穷)为无穷，很容易溢出，所以为了计算时不溢出，就加入减max_value项
	# 次方数减去max_value后，e的该次方数总是在0到1范围内。
	max_value = np.max(logits, axis=1, keepdims=True)
	exp = np.exp(logits - max_value)
	exp_sum = np.sum(exp, axis=1, keepdims=True)
	dist = exp / exp_sum
	return dist


def remove_blank(labels, blank=0):
	new_labels = []
	# 合并相同的标签
	previous = None
	for l in labels:
		if l != previous:
			new_labels.append(l)
			previous = l
	# 删除blank
	new_labels = [l for l in new_labels if l != blank]

	return new_labels


def insert_blank(labels, blank=0):
	new_labels = [blank]
	for l in labels:
		new_labels += [l, blank]
	return new_labels


def beam_decode(y, beam_size=10):
	# y是个二维数组，记录了所有时刻的所有项的概率
	T, V = y.shape
	# 将所有的y中值改为log是为了防止溢出，因为最后得到的p是y1..yn连乘，且yi都在0到1之间，可能会导致下溢出
	# 改成log(y)以后就变成连加了，这样就防止了下溢出
	log_y = np.log(y)
	# 初始的beam
	beam = [([], 0)]
	# 遍历所有时刻t
	for t in range(T):
		# 每个时刻先初始化一个new_beam
		new_beam = []
		# 遍历beam
		for prefix, score in beam:
			# 对于一个时刻中的每一项(一共V项)
			for i in range(V):
				# 记录添加的新项是这个时刻的第几项，对应的概率(log形式的)加上新的这项log形式的概率(本来是乘的，改成log就是加)
				new_prefix = prefix + [i]
				new_score = score + log_y[t, i]
				# new_beam记录了对于beam中某一项，将这个项分别加上新的时刻中的每一项后的概率
				new_beam.append((new_prefix, new_score))
		# 给new_beam按score排序
		new_beam.sort(key=lambda x: x[1], reverse=True)
		# beam即为new_beam中概率最大的beam_size个路径
		beam = new_beam[:beam_size]

	return beam


np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
beam_chosen = beam_decode(y_test, beam_size=100)
for beam_string, beam_score in beam_chosen[:20]:
	print(remove_blank(beam_string), beam_score)

前缀束搜索

在路径中存在何以合并的路径，beamsearch没有考虑这种情况，这就导致丢失了一部分信息。

基本思想是记录prefix的时候，不记录原始的序列，转而记录去除blank和duplicate的序列，这样就可以在搜索的过程中不断合并相同的前缀。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121

import numpy as np
from collections import defaultdict

ninf = float("-inf")


# 求每一列(即每个时刻)中最大值对应的softmax值
def softmax(logits):
	# 注意这里求e的次方时，次方数减去max_value其实不影响结果，因为最后可以化简成教科书上softmax的定义
	# 次方数加入减max_value是因为e的x次方与x的极限(x趋于无穷)为无穷，很容易溢出，所以为了计算时不溢出，就加入减max_value项
	# 次方数减去max_value后，e的该次方数总是在0到1范围内。
	max_value = np.max(logits, axis=1, keepdims=True)
	exp = np.exp(logits - max_value)
	exp_sum = np.sum(exp, axis=1, keepdims=True)
	dist = exp / exp_sum
	return dist


def remove_blank(labels, blank=0):
	new_labels = []
	# 合并相同的标签
	previous = None
	for l in labels:
		if l != previous:
			new_labels.append(l)
			previous = l
	# 删除blank
	new_labels = [l for l in new_labels if l != blank]

	return new_labels


def insert_blank(labels, blank=0):
	new_labels = [blank]
	for l in labels:
		new_labels += [l, blank]
	return new_labels


def _logsumexp(a, b):
	'''
	np.log(np.exp(a) + np.exp(b))

	'''

	if a < b:
		a, b = b, a

	if b == ninf:
		return a
	else:
		return a + np.log(1 + np.exp(b - a))


def logsumexp(*args):
	'''
	from scipy.special import logsumexp
	logsumexp(args)
	'''
	res = args[0]
	for e in args[1:]:
		res = _logsumexp(res, e)
	return res


def prefix_beam_decode(y, beam_size=10, blank=0):
	T, V = y.shape
	log_y = np.log(y)
	# 最后一个字符是blank与最后一个字符为non-blank两种情况
	beam = [(tuple(), (0, ninf))]
	# 对于每一个时刻t
	for t in range(T):
		# 当我使用普通的字典时，用法一般是dict={},添加元素的只需要dict[element] =value即可，调用的时候也是如此
		# dict[element] = xxx,但前提是element字典里，如果不在字典里就会报错
		# defaultdict的作用是在于，当字典里的key不存在但被查找时，返回的不是keyError而是一个默认值
		# dict =defaultdict( factory_function)
		# 这个factory_function可以是list、set、str等等，作用是当key不存在时，返回的是工厂函数的默认值
		# 这里就是(ninf, ninf)是默认值
		new_beam = defaultdict(lambda: (ninf, ninf))
		# 对于beam中的每一项
		for prefix, (p_b, p_nb) in beam:
			for i in range(V):
				# beam的每一项都加上时刻t中的每一项
				p = log_y[t, i]
				# 如果i中的这项是blank
				if i == blank:
					# 将这项直接加入路径中
					new_p_b, new_p_nb = new_beam[prefix]
					new_p_b = logsumexp(new_p_b, p_b + p, p_nb + p)
					new_beam[prefix] = (new_p_b, new_p_nb)
					continue
				# 如果i中的这一项不是blank
				else:
					end_t = prefix[-1] if prefix else None
					# 判断之前beam项中的最后一个元素和i的元素是不是一样
					new_prefix = prefix + (i,)
					new_p_b, new_p_nb = new_beam[new_prefix]
					# 如果不一样，则将i这项加入路径中
					if i != end_t:
						new_p_nb = logsumexp(new_p_nb, p_b + p, p_nb + p)
					else:
						new_p_nb = logsumexp(new_p_nb, p_b + p)
					new_beam[new_prefix] = (new_p_b, new_p_nb)
					# 如果一样，保留现有的路径，但是概率上要加上新的这个i项的概率
					if i == end_t:
						new_p_b, new_p_nb = new_beam[prefix]
						new_p_nb = logsumexp(new_p_nb, p_nb + p)
						new_beam[prefix] = (new_p_b, new_p_nb)

		# 给新的beam排序并取前beam_size个
		beam = sorted(new_beam.items(), key=lambda x: logsumexp(*x[1]), reverse=True)
		beam = beam[:beam_size]

	return beam


np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
beam_test = prefix_beam_decode(y_test, beam_size=100)
for beam_string, beam_score in beam_test[:20]:
	print(remove_blank(beam_string), beam_score)

特点

ctc假设输出是相互独立的，所以没有办法学习到输出的上下文关系，也就是缺失了语言模型 ctc的对齐方式是单调的，适用于语音识别但是对于其他诸如翻译等场景是不适合的 ctc的输入与输出是多对一的关系.输入序列的长度一定大于等于输出长度。

参考

  1. 李理的博客ctc
  2. ctcloss
  3. ctcloss解释
  4. logSumExp()的作用
FEATURED TAGS
数学 工具 推荐系统 llms 机器学习 开发 深度学习 语音识别 nlp 搜索 spark 数据分析 开发语言 bert 信息抽取 数据结构 project