定义
AB测试是为明确某个问题,制作两个(A/B)或多个(A/B/n)版本,在同一时间维度,分别让组成成分相同(相似)的访客群组(目标人群)随机的访问这些版本,收集各群组的用户体验数据和业务数据;最后分析、评估出最好版本,正式采用。
基础概念
正交试验与互斥实验
一个产品的流量是有限的,但是A/B实验的需求是大量的,因此在进行实验前需要确认流量必须互斥还是可以进行正交。正交实验指每个独立实验为一层,层与层之间流量是正交的,一份流量经过每层实验时,都会再次随机打散,且随机效果离散。互斥实验指实验在同一层拆分流量,且不论如何拆分,不同组的流量是不重叠的,如下图所示:
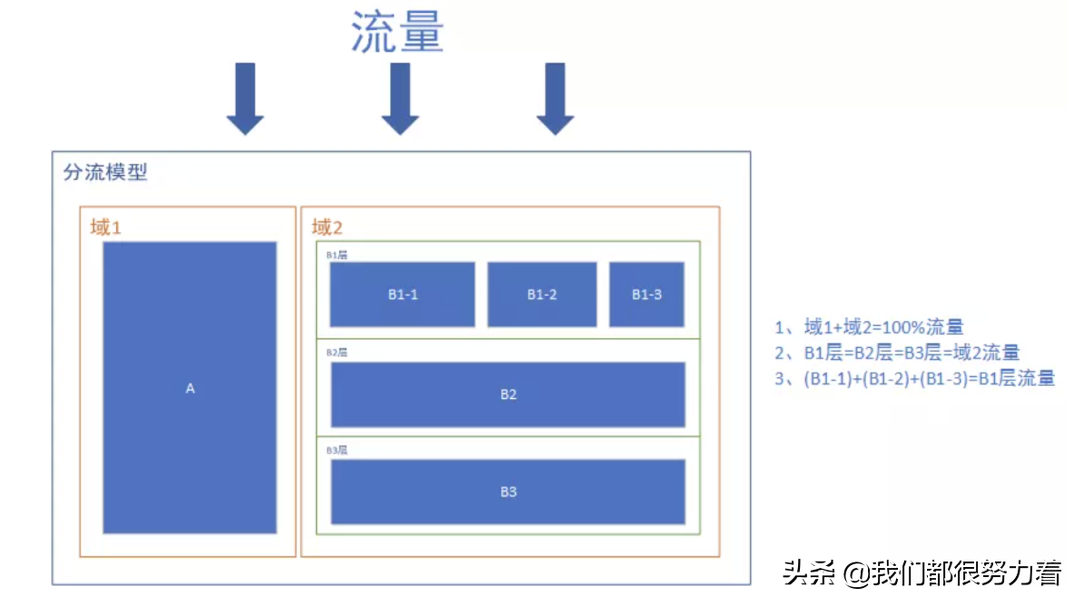
简单来说互斥试验就是在测试的功能会因为重叠流量相互干扰,所以需要流量完全不同 正交试验指的是,比如在ui层、后端都需要测试,ui层和后端所使用的流量一致,只是在经过每一个测试部分的时候重新打乱分组。也就是说ui和后端流量一致,但是分组流量正交。
实验分组
一般来说,至少有1个实验组A和1个对照组B,但是随着A/B测试的应用越来越广泛,并不局限于只有1个实验组A和1个对照组B,可能会有实验组A1、实验组A2和对照组B,甚至更多的实验组同时验证不同策略的效果。比如在实际的运营工作中,需要评估某个券的效果,这时候设置了3个组:
- 实验组1:用规则发券,所有目标用户群发放满200-20的品类券
- 实验组2:走模型策略,基于用户的标签属性发放不同门槛-面额的券,比如有人发放满150-10,有人发放满300-30
- 对照组:不进行任何发券动作
这样,根据实验组1和对照组进行比较能得出规则发券的效果,实验组2和对照组进行比较能得出模型策略发券效果,从而得出走模型策略相较于规则发券效果提升了多少。
假设检验
假设检验是先对总体参数提出一个假设值,然后利用样本信息判断这一假设是否成立。需要了解假设检验中的两个假设、两类错误。
两个假设
- 原假设H0:实验中想反对的假设
- 备择假设H1:实验中想予以支持的假设
两类错误
- 第一类错误:弃真错误,当原假设为真时拒绝原假设
- 第二类错误:取伪错误,当原假设为假时未拒绝原假设
假设检验中的P值
统计显著性指标的数值等于1减去统计学假设检验中的P值(p-value),P值表示样本间的差异由随机因素所导致的概率。
置信度
置信区间计算: \(\left[\mu-1.96 * \frac{\sigma}{\sqrt{n}}, \quad \mu+1.96 * \frac{\sigma}{\sqrt{n}}\right]\)