无条件下的极值
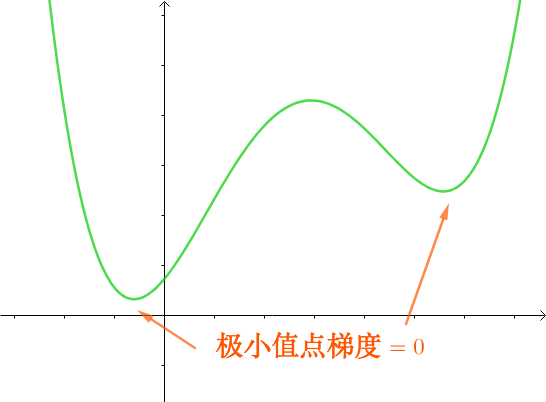
直观
根据梯度意义,在函数的极值点梯度为0:
代数
求极小值:$minimize f(x)$.需要求解$\nabla f=0$
单等式约束下的极值
直观
代数
多等式约束下的极值
不等式约束下的极值
比如我们要求刚才同心圆的最小值,那就是圆点了,半径为0肯定就是最小值,从代数上看就是$minimize f(x, y) = x^2 + y^2$
解:$\nabla f=0 \Longrightarrow(x, y)=(0,0)$
情况一
添加一个不等式约束,如: \(\begin{array}{ll} \operatorname{minimize} & f(x, y) \\ \text { subject to } & h(x, y)=x+y \leq 1 \end{array}\)
可以看到,这个不等式约束实际上包含了原点:
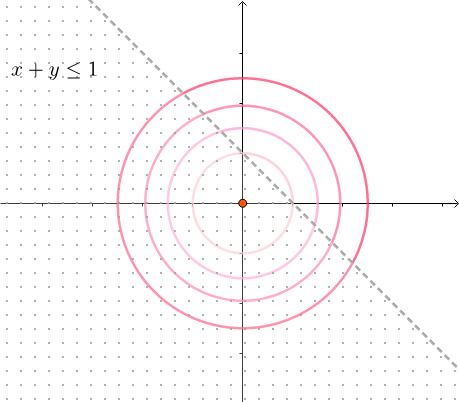
所以这个约束等于没有,依然求解:$\nabla f=0 \Longrightarrow(x, y)=(0,0)$
情况二
换一个约束:
\(\begin{array}{ll}
\operatorname{minimize} & f(x, y) \\
\text { subject to } & h(x, y)=x+y \leq-2
\end{array}\)
如下图所示:

因为同心圆是凸函数的等高线,所以等高线的值是如下图排列的:

所以,早不等式约束下,最小值是在边缘相切的地方取得。和用等式$x+y=-2$进行约束效果是一样的。
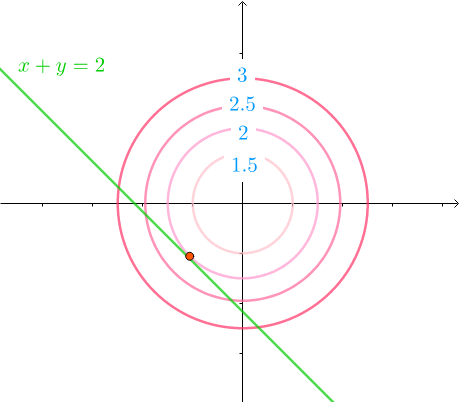
因此可以通过解方程组求出答案: \(\left\{\begin{array}{l} \nabla f+\mu \nabla h=0 \\ h(x, y)=x+y=-2 \end{array}\right.\)
新增的条件
同心圆是凸函数的等高线,等高线的值如下排列,所以在相切处,法线也就是$\nabla f$的方向如下(法线也就是梯度,指向增长最快的方向,也就是等高线的值变大的方向):
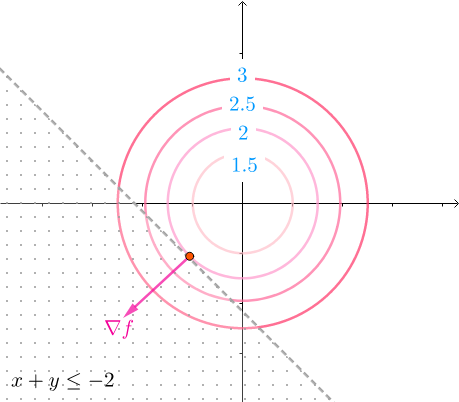
而凸函数h(x,y)的法线$\nabla h$也一样指向h(x,y)增长的方向,这个方向正好和$\nabla f$相反:
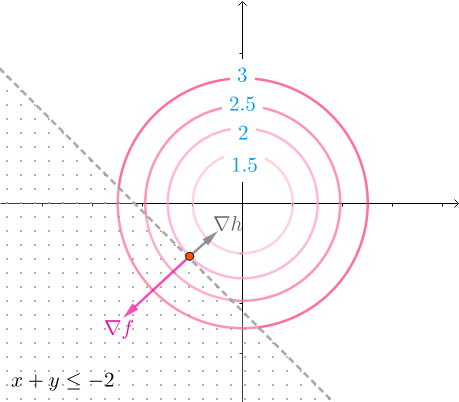
因此:$\nabla f+\mu \nabla h=0, \mu \geq 0$,其中$\mu >=0$表示$\nabla f , \nabla h$方向相反。
因此刚才的方程组可以再增加一个条件: \(\left\{\begin{array}{l} \nabla f+\mu \nabla h=0 \\ h(x, y)=x+y=-2 \\ \mu \geq 0 \end{array}\right.\)
kkt条件
综上,可以把求极值: \(\begin{array}{ll} \operatorname{minimize} & f \\ \text { subject to } & g_{i}=0, i=1,2, \cdots, n \\ & h_{i} \leq 0, i=1,2, \cdots, n \end{array}\) 通过求解如下方程组得到答案: \(\left\{\begin{array}{l} \nabla f+\sum_{i}^{n} \lambda_{i} \nabla g_{i}+\sum_{j}^{m} \mu_{j} \nabla h_{j}=0 \\ g_{i}=0, i=1,2, \cdots, n \\ h_{j} \leq 0, j=1,2, \cdots, m \\ \mu_{j} \geq 0 \\ \mu_{j} h_{j}=0 \end{array}\right.\) 这个就是kkt条件
