混淆矩阵
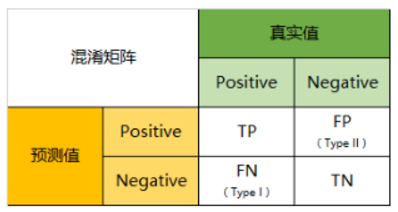
正例预测为正例则为true positive:TP 负例预测为负例则为true negative:TN 负例预测为正例则为flase positive:FP 正例预测为负例则为flase negative:FN
准确率错误率
准确率:E= FP+FN / M 错误率: A = TP+TN / M M = TP+TN+FP+FN
缺点:对样本不平衡的问题,无法给出客观的评价
精确率召回率
精确率P:TP/TP+FP 召回率R:TP/TP+FN F1:精确率 * 召回率 * 2 /(精确率+召回率),F1值为精确率和召回率的调和平均值 ROC: \(F_{\beta} = \frac{(1+\beta ^2)*P*R}{(\beta ^2 * P) + R}\) 其中如果$\beta>0$,度量了P和R的相对重要性,当$\beta=1$为F1,当$\beta>1$,R更重要,相反P更重要。
ROC
TPR = TP / TP+FN 真正率,和上面的召回率定义相同 FPR = FP / TN + FN 假正率
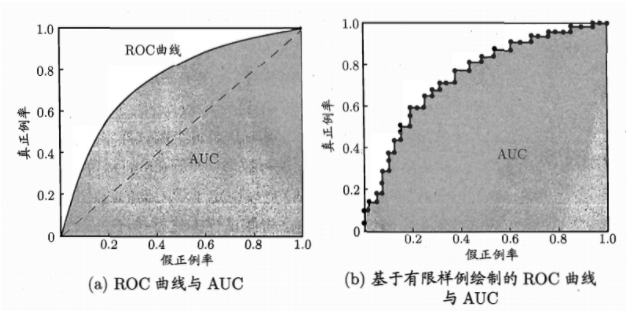
解释:90%的正样本,10%的负样本,用准确率不妥当。 TPR只关注90%正样本中有多少被真正覆盖 FPR只关注10%负样本有多少被错误覆盖
FPR表示模型虚报的响应程度,而TPR表示模型预测响应的覆盖程度。TPR越高,同时FPR越低(即ROC曲线越陡),那么模型的性能就越好。
所以如果A的ROC包裹B的ROC,则A学习器更好。 如果A,B有交叉,则不能断言,这时候引入了AUC值。
AUC
ROC曲线图对角线,它的面积正好是0.5。对角线的实际含义是:随机判断响应与不响应,正负样本覆盖率应该都是50%,表示随机效果。ROC曲线越陡越好,所以理想值就是1,一个正方形,而最差的随机判断都有0.5,所以一般AUC的值是介于0.5到1之间的。
AUC的一般判断标准: 0.5 - 0.7:效果较低,但用于预测股票已经很不错了 0.7 - 0.85:效果一般 0.85 - 0.95:效果很好 0.95 - 1:效果非常好,但一般不太可能
NDCG
CG(累计增益)只考虑相关性的关联程度,不考虑位置因素,是一个搜索结果相关性分数的综合,指定位置p的CG为$CG_p = \sum_{i=1}^p rel_i$ $rel_i$代表i这个位置上的相关度
例如:搜索篮球,最理想的结果是B1 B2 B3,而出现的结果为B3 B1 B2,CG的值是没有变化的,因此需要DCG
DCG(折损累计增益)在每一个CG的结果上加一个折损值,目的是为了让排名靠前的结果越能影响最后的结果,假设排序越往后,价值越低,到第i个位置,它的价值为$frac{1}{log_2(i+1)}$,那么第i个结果产生的增益为$rel_i * frac{1}{log_2(i+1)}$。所以$DCG_p = \sum_{i=1}^p rel_i * \frac{1}{log_2(i+1)} = rel_1 + \sum_{i=2}^p rel_i * \frac{1}{log_2(i+1)}$
当然还有一种比较常用的公式,用来增加相关度影响比重DCG的计算方式是$DCG_p = \sum_{i=1}^p \frac{2^{rel_i}}{log_2(i+1)}$
NDCG(归一化折损累计增益):是归一化的DCG,由于搜索结果随着检索词的不同,返回的数量是不一致的,而DCG是一个累加的值,没有办法针对两个不同的搜索结果进行比较,因此需要归一化处理。 \(NDCG_p = \frac{DCG_p}{IDCG_p}\) $IDCG_p$是理想情况下最大的DC的值 \(IDCG_p = \sum_{i=1}^{REL} \frac{2^{rel_i} - 1}{log_2 (i+1)}\) 其中REL表示,结果按照相关性从大到小的顺序排序,取前p个结果组成的集合,也就是按照最优的方式对结果进行排序。
例如:搜索的结果有5个,相关性分数为3,2,3,0,1,2
那么CG=3+2+3+0+1+2=11
可以看到只是对相关的分数进行了一个关联的打分,并没有召回的所在位置对排序结果评分对影响。而我们看DCG:
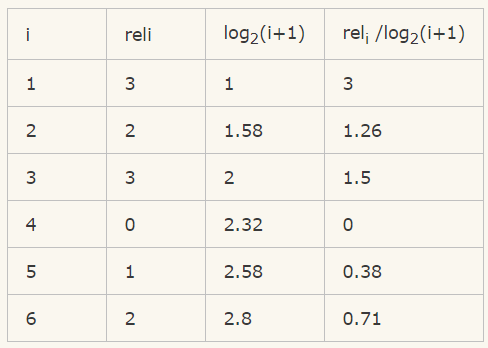
所以 DCG = 3+1.26+1.5+0+0.38+0.71 = 6.86
接下来我们归一化,归一化需要先结算 IDCG,假如我们实际召回了8个物品,除了上面的6个,还有两个结果,假设第7个相关性为3,第8个相关性为0。那么在理想情况下的相关性分数排序应该是:3、3、3、2、2、1、0、0。计算IDCG@6:
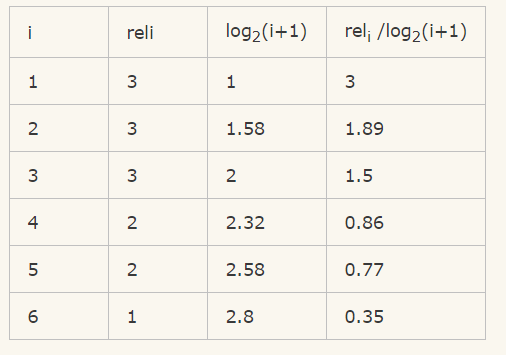
所以IDCG = 3+1.89+1.5+0.86+0.77+0.35 = 8.37 最终 NDCG@6 = 6.86/8.37 = 81.96%
多类分类
macro-average:
1
所有类的F1加和求平均
micro-average:
1
(TP + FP) / (TP + TN + FP + FN)
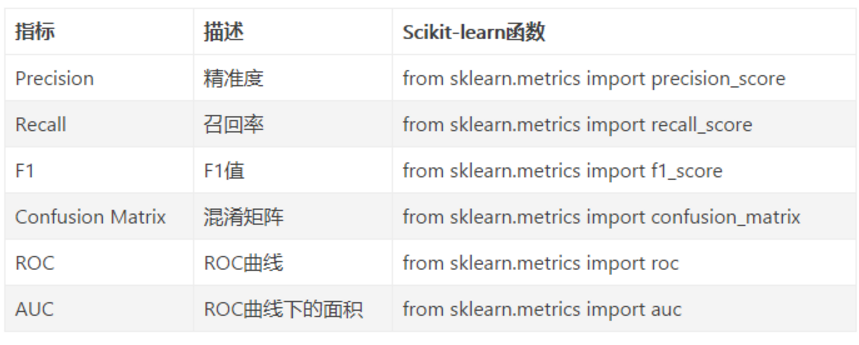
sklearn中的评价指标