基础概念
PCA作为一种常见的数据分析方式,常用于高维数据的降维,用于提取数据的主要特征分量。
内积
两个向量的A和B的内积的形式如下:
\(\left(a_{1}, a_{2}, \cdots, a_{n}\right) \cdot\left(b_{1}, b_{2}, \cdots, b_{n}\right)^{\top}=a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n}\)
内积运算将两个向量映射为实数。
从集合角度来看,假设AB为二维向量,则:
\(A=\left(x_{1}, y_{1}\right), \quad B=\left(x_{2}, y_{2}\right) A \cdot B=|A||B| \cos (\alpha)\)
几何表示为:
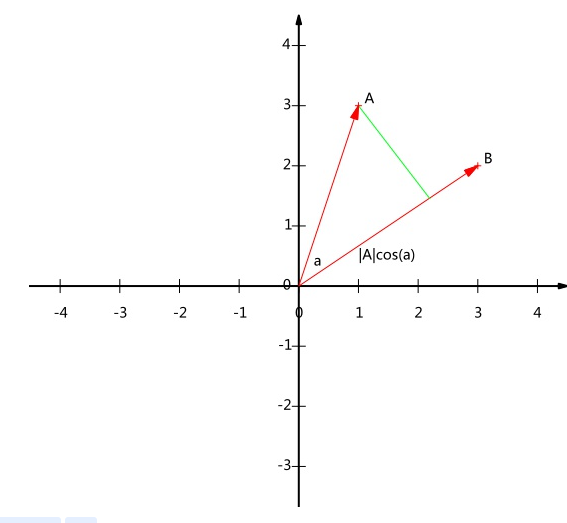
我们看到AB的内积等于A到B的投影长度乘以B的模,如果假设B的模为1,则$A.B=Acos(a)$ 也就是说,AB的内积的值等于A向B所在直线投影的标量的大小
基
在一般的坐标系中,向量(3,2)其实就隐含一个定义:以X和Y轴为正方向长度为1的向量为标准,向量(3,2)就是说在X轴投影为3,在Y轴投影为2.
所以对于(3,2)相求其在(1,0),(0,1)这组基下坐标的话,分别内积就是了。 因此:要准确描述一个向量,首先确定一组基,然后给出在基所在的各个直线上的投影,就定为一个向量。
如向量(3,2)在$\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right), \left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$这组基的坐标: \(\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ -1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right)\left(\begin{array}{l} 3 \\ 2 \end{array}\right)=\left(\begin{array}{c} 5 / \sqrt{2} \\ -1 / \sqrt{2} \end{array}\right)\)
最大可分性
如果基的数量小于向量本身的维数,是不是就可以达到降维的效果? 如何选取最优的基? 直观的想法:投影后尽可能分散,防止样本消失。 方差,协方差
PCA求解
PCA的目的是降维,在最大可分性的分析中可以发现,目标转换为变量内方差以及变量间的协方差有关,最大化方差,同时使得协方差为0.
假设矩阵X: \(X=\left(\begin{array}{llll} a_{1} & a_{2} & \cdots & a_{m} \\ b_{1} & b_{2} & \cdots & b_{m} \end{array}\right)\) 然后: \(\frac{1}{m} X X^{\top}=\left(\begin{array}{cc} \frac{1}{m} \sum_{i=1}^{m} a_{i}^{2} & \frac{1}{m} \sum_{i=1}^{m} a_{i} b_{i} \\ \frac{1}{m} \sum_{i=1}^{m} a_{i} b_{i} & \frac{1}{m} \sum_{i=1}^{m} b_{i}^{2} \end{array}\right)=\left(\begin{array}{cc} \operatorname{Cov}(a, a) & \operatorname{Cov}(a, b) \\ \operatorname{Cov}(b, a) & \operatorname{Cov}(b, b) \end{array}\right)\) 可以发现,对角线上是方差,其他的元素为协方差。
根据最终的目的,我们需要将出对角线外的元素化为0,并且在对角线上将元素按从大到小从上到下排列。
假设原始数据矩阵X对应的协方差矩阵为C,而P是一组基按照行组成的矩阵,设Y=PX,则Y为X对P做基变换后的数据,设Y的协方差矩阵为D,则: \(\begin{aligned} D &=\frac{1}{m} Y Y^{T} \\ &=\frac{1}{m}(P X)(P X)^{T} \\ &=\frac{1}{m} P X X^{T} P^{T} \\ &=P\left(\frac{1}{m} X X^{T}\right) P^{T} \\ &=P C P^{T} \end{aligned}\) 则优化目标转化为寻找矩阵P使得上述结果是一个对角矩阵。
借助线性代数中实对称矩阵的特点:
1
2
1.不同特征值对应的特征向量正交
2.设特征向量重数为r,则必然存在r个线性无关的特征向量,因此可以将这r个特征向量单位正交化。
则:一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,设n个特征向量为$e^1,e^2,…e^n$我们将其按列组成矩阵:$E = (e^1,e^2,…e^n)$
根据协方差矩阵C有如下结论: \(E^{T} C E=\Lambda=\left(\begin{array}{llll} \lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n} \end{array}\right)\)
其中$\Lambda$为对角矩阵,其对角元素为各特征向量对应的特征值。
结论:我们所需要求解的P就是协方差矩阵的特征向量单位化后按照行排列出来的矩阵。
总结
假设有m条n维数据:
1
2
3
4
5
6
1. 将原始数据按照列组成n行m列的矩阵X
2. 将X的每一行进行零均值化
3. 求解协方差矩阵
4. 求出协方差矩阵的特征值以及对应的特征向量
5. 将特征向量按照对应特征值从大到小排列,取前k行组成矩阵P
6. Y=PX即为降维到k维后的数据
性质
1
2
3
4
1. 缓解维度灾难
2. 降噪
3. 过拟合
4. 特征独立
其他
1
2
3
4
5
6
7
8
1. 在验证集和测试集合中的均值都是用的训练集的均值
2. 与SVD相比
特征值和特征向量是针对方阵的,对任意形式的矩阵都可以做奇异值分解
在sklearn中的pca也是通过svd实现的,
因为样本维度高的化,协方差矩阵计算太慢
方阵的矩阵分解计算效率不高
SVD还有迭代求解的方式,效率高
PCA和SVD的右边=奇异向量的压缩效果相同