基本概念
对抗训练是一种增量神经网络鲁棒性的方式,在实现的过程中,通过针对样本的扰动来使得网络进行适应变化,从而对对抗样本具有鲁棒性。
对抗样本一般特征:
1
2
1.相对于原始的输入,所添加的扰动时微小的
2.可以使得模型犯错
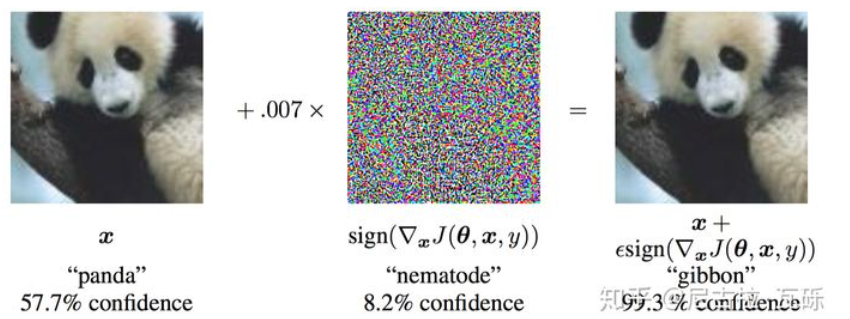
对抗训练概念:在原始的输入x中加入扰动$r_{adv}$,得到对抗样本参加训练。 \(\min _{\theta}-\log P\left(y \mid x+r_{a d v} ; \theta\right)\) 其中,y表示标签,$\theta$为模型的参数,在论文中给出的解释是,神经网络由于其线性的特点,很容易受到线性扰动的干扰,所以提出Fast Gradient Sign Method (FGSM)来进行扰动的计算,扰动定义为: \(r_{a d v}=\epsilon \cdot \operatorname{sgn}\left(\nabla_{x} L(\theta, x, y)\right)\) 其中sign为符号函数,L为损失函数,在论文中指出$\epsilon=0.25$的时候扰动比较成功。
1
对上面扰动的理解:将输入的样本朝着损失上升的方向再进一步,得到的对抗样本就可以造成更大的损失,提高模型的错误率。
攻击模式
白盒攻击:
1
获取到所使用算法的名称以及相关参数,在具体攻击时可以与系统进行交互
黑盒攻击:
1
不了解具体的模型,但仍可同系统进行交互,可以传递输入观测输出
无目标攻击:
1
对一个样本进行对抗样本的生成,促使系统对其分类错误,但是不关注其具体的类别
有目标攻击:
1
对一个样本进行对抗样本的生成,同时还可以指定其所属的类别
对抗学习
在Towards Deep Learning Models Resistant to Adversarial Attacks中总结了对抗学习的一般形式: \(\min _{\theta} \mathbb{E}_{(x, y) \sim \mathcal{D}}\left[\max _{r_{a d v} \in \mathcal{S}} L\left(\theta, x+r_{a d v}, y\right)\right]\) 公式分为两部分,第一部分表示内部的损失函数最大,第二十外部的经验风险最小。同时,内部的max是为了找到最好的扰动形式,L为损失函数,S为扰动的范维空间。外部的min表示在当前所找到的扰动下找到最鲁棒的模型参数,其中D表示输入样本的分布。
传统的对抗学习都是在CV领域的,因为其输入天然的具有连续性,反思NLP问题,由于其输入时离散的单词序列,导致其无法直接在输入上进行扰动。论文Adversarial Training Methods for Semi-Supervised Text Classification中指出可以在连续的embedding中进行扰动。
FGM
1
2
3
4
5
6
对于每个x:
1.计算x的前向loss、反向传播得到梯度
2.根据embedding矩阵的梯度计算出r,并加到当前embedding上,相当于x+r
3.计算x+r的前向loss,反向传播得到对抗的梯度,累加到(1)的梯度上
4.将embedding恢复为(1)时的值
5.根据(3)的梯度对参数进行更新
论文Adversarial Training Methods for Semi-Supervised Text Classification提出Fast Gradient Method(FGM)其假设输入的文本序列为$embedding vectors[v_1,v_2,…,v_T]$为x,embedding的扰动为: \(\begin{aligned} r_{a d v} &=\epsilon \cdot g /\|g\|_{2} \\ g &=\nabla_{x} L(\theta, x, y) \end{aligned}\) 与原始提出的FGSM做了一点改变,取消了符号函数,基于二范式做了一个scale。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import torch
class FGM():
def __init__(self, model):
self.model = model
self.backup = {}
def attack(self, epsilon=1., emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
# 使用
# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
PGD
1
2
3
4
5
6
7
8
对于每个x:
1.计算x的前向loss、反向传播得到梯度并备份
对于每步t:
2.根据embedding矩阵的梯度计算出r,并加到当前embedding上,相当于x+r(超出范围则投影回epsilon内)
3.t不是最后一步: 将梯度归0,根据1的x+r计算前后向并得到梯度
4.t是最后一步: 恢复(1)的梯度,计算最后的x+r并将梯度累加到(1)上
5.将embedding恢复为(1)时的值
6.根据(4)的梯度对参数进行更新
论文Towards Deep Learning Models Resistant to Adversarial Attacks中提出Projected Gradient Descent(PGD)。相较于FGM的一步到位,PGD的实现方式是多步走,如果走出扰动半径就拉回。 \(\begin{aligned} x_{t+1} &=\Pi_{x+\mathcal{S}}\left(x_{t}+\alpha g\left(x_{t}\right) /\left\|g\left(x_{t}\right)\right\|_{2}\right) \\ g\left(x_{t}\right) &=\nabla_{x} L\left(\theta, x_{t}, y\right) \end{aligned}\) 其中$\mathcal{S}=r \in \mathbb{R}^{d}:|r|_{2} \leq \epsilon$为扰动的约束空间,$\alpha$为小步的步长。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import torch
class PGD():
def __init__(self, model):
self.model = model
self.emb_backup = {}
self.grad_backup = {}
def attack(self, epsilon=1., alpha=0.3, emb_name='emb.', is_first_attack=False):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, epsilon)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
r = param_data - self.emb_backup[param_name]
if torch.norm(r) > epsilon:
r = epsilon * r / torch.norm(r)
return self.emb_backup[param_name] + r
def backup_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
self.grad_backup[name] = param.grad.clone()
def restore_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
param.grad = self.grad_backup[name]
# 使用
pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
pgd.backup_grad()
# 对抗训练
for t in range(K):
pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
if t != K-1:
model.zero_grad()
else:
pgd.restore_grad()
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
pgd.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
FreeAT
1
2
3
4
5
6
7
初始化r=0
对于epoch=1...N/m:
对于每个x:
对于每步m:
1.利用上一步的r,计算x+r的前后向,得到梯度
2.根据梯度更新参数
3.根据梯度更新r
论文Adversarial Training for Free!提出FreeAT (Free Adversarial Training)。核心点在于优化PGD扰动的计算效率。 缺点:
1
FreeLB指出,FreeAT的问题在于每次的r对于当前的参数都是次优的(无法最大化loss),因为当前r是由r(t-1)和theta(t-1)计算出来的,是对于theta(t-1)的最优。