概述
起源于赌博学:一个赌徒在摇老虎机的时候,发现有一排一样的老虎机,但是每台机器的中奖概率不一样,当然赌徒也不知道真实的老虎机中奖的概率分布,那么如何才可以实现最大化摇动老虎机的收益,这就是多臂老虎机问题:Multi-armed bandit problem, K-armed bandit problem, MAB
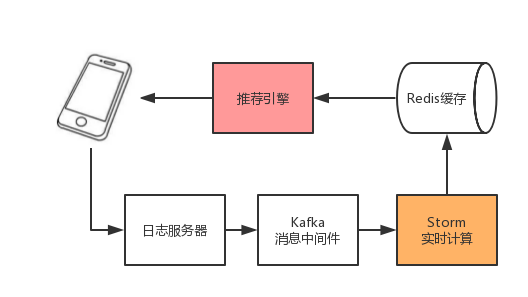
 类比如推荐系统:
类比如推荐系统:
1
2
3
4
1.对新用户如何快速的了解其兴趣爱好
2.如何科学的进行商品多样性的增加
3.对于丰富的广告库或者商品库,如何了解为那些用户展示那些商品或者广告,如果每次都拿最好的,那那些新的广告就永远不会被展示
4.新训练一个模型有什么方法可以比abtest更快的了解那个模型较优
探索和利用
Exploration and Exploitation(EE问题,探索与开发):
1
2
1.探索:用户会对所推荐的商品失去兴趣,需要不断的探索用户新的兴趣
2.开发:对用户感兴趣的尽可能的利用
bandit与推荐系统
对于新用户来说,怎么通过多次试验来有目的的对其兴趣进行建模:
1
2
3
用topic表示用户的兴趣,对应MAB中的Arm,通过若干次实验,对新用户的兴趣爱好进行刻画,了解其对每个topic的感兴趣概率。
如果用户对某个topic感兴趣,就表示有了收益,如果不感兴趣就产生遗憾。
经过选择-观察-更新-选择的循环,理论上就会逼近用户的兴趣点。
累计遗憾
通常通过累计遗憾regret来 表示 Bandit算法的效果 \(R_{T}=\sum_{i=1}^{T}\left(w_{o p t}-w_{B(i)}\right)=T \cdot W^{*}-\sum_{i=1}^{T} w_{B(i)}\) 其中$w_{B(i)}$是第i次试验中被选中的臂的期望收益,$w^*$是所有臂中最优的哪一个。用不同的Bandit算法进行相同次数的试验,看regret增长慢的是哪一个。
Bandit
首先随机的试验,然后进行平均收益的计算,一直选取平均收益最大的臂
Epsilon-Greedy
在0-1之间选取$\epsilon$,每次都以$\epsilon$的概率在所有臂中选取一个,然后通过$1 - \epsilon$选取截止当前平均收益最大的臂,依据回报的结果进行收益的更新。 基本思想: 1.以ε的概率选择探索 (Exploration):从N个item中选择一个给到user,根据反馈更新每个item的被选择的概率。 2.以1-ε的概率选择利用 (Exploitation):从N个item中选择最好的item推荐给用户。 存在问题: 1.在推荐次数相同的情况下,好和不好的item被探索推荐的概率是一样的 2.在推荐的成功概率相同的情况下,被推荐次数多的和次数少的item得到再被推荐的概率是一样的
Thompson sampling
Thompson sampling算法用到了Beta分布,其中假设每个臂是否产生收益,其背后是有一个概率分布,而产生的收益P是符合Beta(wins,lose)分布,每一个臂都维护一套Beta分布的参数,在每次试验之后,选中其中的某个臂摇一下,有收益的臂win加1,否则lose加1
Beta分布
定义域:[0,1]
参数:$\alpha , \beta$,都是正数,称之为形状参数,不同的组合有不同的宽窄以及平移情况
概率密度函数:
\(f(x ; \alpha, \beta)=\frac{1}{B(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}\)
其中$\Gamma$为Gamma函数,是阶乘的扩展
\(\Gamma(x)=\int_{0}^{+\infty} t^{x-1} e^{-t} \mathrm{~d} t(x>0)\)
Beta的方差为:
\(\frac{\alpha \beta}{(\alpha+\beta)^{2}(\alpha+\beta+1)}\)
Beta的均值为:
\(\frac{\alpha}{\alpha+\beta}\)
Beta分布的图形:
 从图中可以看出
从图中可以看出
1
2
1.均值越大,概率密度分布的中心位置越靠近1,结果就是所产生的值大多数都靠近1,反之则靠近0
2.均值的分母越大,表示分布越窄,则产生的数越集中于中心位置。
UCB
全称为Upper Confidence Dound 置信区间上界。具体的步骤是:对每个臂都尝试一下,然后在其他的时刻基于以下公式更新计算每个臂的分数,然后选择其中分数最大的臂作为选择: \(\bar{x}_{j}+\sqrt{\frac{2 \ln t}{T_{j}}}\)
\(a*{x}_{u,j}+b*\sqrt{\frac{2 \ln t_{u,j}}{T_{j}}}\)
1
2
基本思想:对某个item尝试的次数越多则对该item回报估计的置信区间越窄,估计的不确定性也就减小。从而均值大的item被选择的次数增多(exploitation)。对某些item的尝试次数较少,则其置信区间较宽,不确定高,则置信区间宽的item被倾向选择(exploration)
分母为item j的曝光次数,分子为总的曝光次数
示例:
1
假设现在摇一次骰子得到的点数为2,则均值为2,实际上均值为3.5,但是显然这个估计不靠谱,可以用置信区间来衡量变化的估计,均值为2,其95置信区间的上下限为分别5.2、1.4
LinUCB
优化ucb算法的上下文无关,不关注面临的用户或者商品具体是什么的问题。
1
假设在对user推送item的时候,其反馈和相关的特征有线性关系
在时间t,对于用户$u_t$,可选择的商品a的特征向量为$x_{t,a}$,$x_{t,a}$作为上下文信息,表示用户和商品的特征。算法依据历史的反馈进行item的选择$a_t$,同时收到用户的反馈收益$r_{t,a_t}$,$r_{t,a_t}$的期望由用户和商品共同决定,然后依据反馈$(x_{t,a},a_t,r_{t,a_t})$对候选排序进行改进,目标是使得整个过程中的损失最小,也就是遗憾最小$R_A(T)$。 \(R_{A}(T)=E\left[\sum_{t=1}^{T} r, a_{t}^{*}\right]-E\left[\sum_{t=1}^{T} r, a_{t}\right]\) 其中T表示实验的总步数,$a^$表示在时间t是最大的收益的arm。 LinUCB中,设定的是每一个arm的期望收益和特征向量为线性关系的。 \(E\left[r_{t, a} \mid x_{t, a}\right]=x_{t, a}^{T} \theta_{a}\) 其中$\theta_{a}$是模型的参数,维度为d,每一个arm都维护一个$\theta_{a}$ 对于单个arm,通过前m个comtext向量组成的矩阵为$D_a$,维度为mn。前m个收益组成的向量为$C_a$。基于平方误差函数: \(\operatorname{loss}=\sum_{i=1}^{m}\left(c_{a, i}-\sum_{j=0}^{d} \theta_{a, j} x_{i j}\right)^{2}+\lambda \sum_{j=0}^{d} \theta_{a, j}^{2}\) 其中$\lambda$是正则项系数,求损失函数的最小值,对$\theta_{a}$求导: \(\nabla_{\theta_{a}} \text { loss }=2 D_{a}^{T}\left(c_{a}-D_{a} \theta_{a}\right)+2 \lambda \theta_{a}\) 令$\nabla_{\theta_{a}} \operatorname{loss}=0, \lambda=1$,可知: \(\theta_{a}=\left(D_{a}^{T} D_{a}+I\right)^{-1} D_{a}^{T} c_{a}\) 基于岭回归可以得到$\theta_{a}$的概率分布是高斯分布: \(\theta_{a} \sim N\left(\left(D_{a}^{T} D_{a}+I\right)^{-1} D_{a}^{T} c_{a},\left(D_{a}^{T} D_{a}+I\right)^{-1}\right)\) 令其中: \(\begin{aligned} \hat{\theta}_{a} &=\left(D_{a}^{T} D_{a}+I\right)^{-1} D_{a}^{T} c_{a} \\ A_{a} &=D_{a}^{T} D_{a}+I \end{aligned}\) 可得$\theta_{a}$的概率分布为$\theta_{a} \sim N\left(\hat{\theta}{a}, A{a}^{-1}\right)$ 于是在第t时刻可以得到$x_{t, a}^{T} \theta_{a} \sim N\left(x_{t, a}^{T} \hat{\theta}{a}, x{t, a}^{T} A_{a}^{-1} x_{t, a}\right)$,也就是$r_{t, a} \sim N\left(x_{t, a}^{T} \hat{\theta}{a}, x{t, a}^{T} A_{a}^{-1} x_{t, a}\right)$ 依据高斯分布的性质,得到置信上界就可以基于一般的UCB进行更新: \(x_{t, a}^{T} \hat{\theta}_{a}+\alpha \sqrt{\left.x_{t, a}^{T} A_{a}^{-1} x_{t, a}\right)}\)
计算流程
设定$\alpha$ For t = 1,2,3,…. 用户数 对所有得arm也就是商品获取context For all a: if a is new: 设置$A_a$为单位矩阵 设置$b_a$为d维向量 计算$\hat{\theta}{a} = A{a}^{-1} b_a$ 计算上界$P_{t,a} = x_{t, a}^{T} \hat{\theta}{a}+\alpha \sqrt{\left.x{t, a}^{T} A_{a}^{-1} x_{t, a}\right)}$ 选择最大上界$P_{t,a}$对应得arm也就是$a_t$,并得到对应得$r_t$ 更新$A_{a_{t}}=A_{a_{t}}+x_{t, a_{t}} x_{t, a_{t}}^{T}$ 更新$b_{a_{t}}=b_{a_{t}}+r_{t} x_{t, a_{t}}$ 其中$A_{a_{t}}$的维度为:mm,m表示用户数 $b_{a_{t}}$的维度为:mn,m为用户数,n为商品数