优化方法框架
1.计算目标函数关于参数的梯度:$g_t = \nabla f(w_t)$ 2.根据历史的梯度进行一阶和二阶动量:$m_{t}=\phi\left(g_{1}, g_{2}, \cdots, g_{t}\right) ; V_{t}=\psi\left(g_{1}, g_{2}, \cdots, g_{t}\right)$ 3.计算当前时刻的梯度:$\begin{aligned} \eta_{t} &=\alpha \cdot m_{t} / \sqrt{V_{t}} \end{aligned}$ 4.根据梯度更新参数:$w_{t+1} =w_{t}-\eta_{t}$
1
2
1.一阶动量:表示梯度的移动加权平均,目的在于相互抵消防止震荡。原因在于一阶使得一个向量有不同的方向。
2.二阶动量:表示梯度平方的移动加权,是在向量的模上的累加。将其置于分母可以减小学习率从而减小震荡。
优化方法
GD
1.对于凸函数可以求得最优解,深度学习一般都是非凸问题。 2.计算过程: 1.$g_t = \nabla f(w_t)$ 2.$\eta_{t} =\alpha$ 3.$w_{t+1} = w_{t}-\alpha g_t$ 3.优缺点
1
2
1.优点:可以精细化参数调节、效果会较好,原理直观
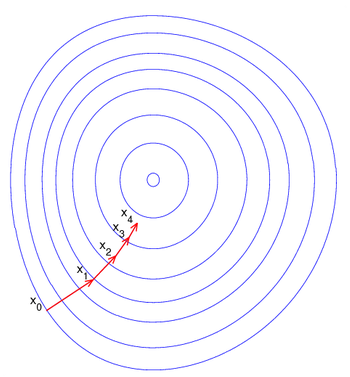
2.缺点:震荡严重,对于每一个参数来说学习率都是一样的,与实际不符。在靠近极小值的时候收敛会变慢。
mini-batch GD
1
2
1.计算的话就和上面类似,每次计算一批的梯度平均值然后更新
2.优化点在于相比较于GD的单样本更新,可以更接近的反应数据真实分布,单样本容易出现很大的偏差。
Momentum
思路:
1
通过指数加权平均来替代当前梯度的更新,从而通过加权平均来抑制震荡,从而达到加速训练的目的。
计算过程 1.$g_t = \nabla f(w_t)$ 2.${m_{t}=\mu * m_{t-1}+(1- \mu)g_{t}}$ 3.$\Delta \theta_{t}=-\eta * m_{t}$ 优缺点:
1
2
1.优点:通过指数加权平均来抑制震荡,从而加速训练
2.缺点:对参数敏感,学习率固定
Nesterov
思路:
1
在计算加权平均的时候,先依据加权平均得到的梯度前进一次,然后再进行加权平均,进而更新。出发点在于对梯度的更新进行修正,避免前进的太快。
计算过程:
1.${g_{t}=\nabla_{\theta_{t-1}} f\left(\theta_{t-1}-\eta * \mu * m_{t-1}\right)}$ 针对上一步加权平均结果进行的前进
2.${m_{t}=\mu * m_{t-1}+(1-\mu )g_{t}}$ 根据上一步结果进行加权平均
3.$\Delta \theta_{t}=-\eta * m_{t}$
 如上图所示:
如上图所示:
1
2
3
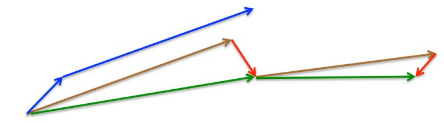
1.蓝色短线为当前梯度,然后计算加权平均前进一步得到长的蓝色
2.然后在前进的方向进行指数加权平均得到棕色的长线
3.最后进行更新校正得到绿色长线
优缺点:
1
2
1.优点:收敛快
2.缺点:计算复杂,学习率固定
Adagrad
思路:
1
对学习率进行约束,从而使得每个参数对应的学习率不同。在初期梯度小的时候可以放大梯度,后期梯度大了可以约束梯度。
计算过程: 1.$n_{t}=n_{t-1}+g_{t}^{2}$ 梯度平方的累加 2.$\Delta \theta_{t}=-\frac{\eta}{\sqrt{n_{t}}+\epsilon} * g_{t}$基于梯度的累加的开方对学习率进行加权。$\epsilon$防止分母为0 优缺点:
1
2
1.优点:在梯度小的时候可以放大梯度,在梯度大的时候可以约束梯度。适用稀疏数据?(因为调整了不同维度的学习率,稀疏数据0较多,频率高,梯度平方和大,学习率会调整变小 )
2.缺点:对全局学习率仍然敏感,正则项可能使得梯度退化为0,使得训练提前结束
RMSprop
思路:
1
对Adagrad改进,将梯度的平方和累加转换为梯度的平方滑动平均
计算过程: 1.$n_{t}=\nu * n_{t-1}+(1-\nu) * g_{t}^{2}$ 梯度平方的滑动平均 2.$\Delta \theta_{t}=-\frac{\eta}{\sqrt{n_{t}+\epsilon}} * g_{t}$基于梯度平方的滑动平均的开方对学习率进行加权。$\epsilon$防止分母为0 优缺点:
1
2
1.优点:基于加权平均的形式可以消除摆动的幅度,使之减小
2.缺点:对全局学习率敏感
Adadelta
思路:
1
2
1.解决adagrad学习率不断减小的问题
2.通过对一个窗口内的梯度进行累加来缓解adagrad的问题
计算过程: \(\Delta \theta_{t} = \frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_t}g_t\) RMS表示指数加权平均。 优缺点:
1
2
1.优点:不需要设置学习率
2.缺点:训练会在最小值附近震动
Adam
思路:
1
将动量加入到RMSprop中,利用一阶距估计和二阶距估计来动态对每个参数进行调整学习率
计算过程: 1.$m_{t}=\mu * m_{t-1}+(1-\mu) * g_{t}$ 梯度的滑动平均 2.$n_{t}=\nu * n_{t-1}+(1-\nu) * g_{t}^{2}$ 梯度评方的滑动平均 3.$\hat{m}{t}=\frac{m{t}}{1-\mu^{t}}$ 滑动平均的修正 4.$\hat{n}{t}=\frac{n{t}}{1-\nu^{t}}$ 滑动平均的修正 5.$\Delta \theta_{t}=-\frac{\hat{m}{t}}{\sqrt{\hat{n}{t}}+\epsilon} * \eta$ 优缺点:
1
2
1.优点:结合了adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点、对内存需求较小、对不同的参数计算不同的自适应学习率、适用于大数据集和高维空间、参数具有确定的范围
2.缺点:二阶动量是在时间窗口内的累加,随着时间窗口的变换,遇到的数据发生巨变,使得滑动平均时大时小,不是单调变换,可能会使得模型震荡,无法收敛。
Adammax
思路:
1
限制adam的学习率提供更为简单的范围
计算过程: 1.$n_{t}=\max \left(\nu * n_{t-1},\left|g_{t}\right|\right)$ 约束值范围 2.$\Delta x=-\frac{\hat{m}{t}}{\hat n{t}+\epsilon} * \eta$ 3.$\hat m_t = \frac{m_t}{1-u^t}$ 4.$m_{t}=\mu * m_{t-1}+(1-\mu) * g_{t}$ 5.$n_{t}=\nu * n_{t-1}+(1-\nu) * g_{t}^{2}$ 优缺点:
1
2
1.优点:解决adam中动量比较小的时候训练缓慢的问题,替换为梯度
2.缺点:仍然可能错过全局最优解
Nadam
思路:
1
带有Nesterov动量项的Adam
计算过程: 1.$m_{t}=\mu * m_{t-1}+(1-\mu) * g_{t}$ 梯度的滑动平均 2.$n_{t}=\nu * n_{t-1}+(1-\nu) * g_{t}^{2}$ 梯度评方的滑动平均 3.$\hat{m}{t}=\frac{m{t}}{1-\mu^{t}}$ 滑动平均的修正 4.$\hat{n}{t}=\frac{n{t}}{1-\nu^{t}}$ 滑动平均的修正 5.$\bar{m}{t}=\left(1-\mu_t\right) * {g}{t}+\mu_{t+1} * \hat{m}{t}$加入Nesterov 6.$\Delta \theta{t}=-\eta * \frac{\bar{m}{t}}{\sqrt{\hat{n{t}}}+\epsilon}$ 优缺点:
1
2
1.优点:加速了adam
2.缺点:仍然可能错过全局最优解
RAdam
思路:
1
根据方差分散度动态的打开或者关闭自适应学习率,并提出一种不需要可调参数学习预热的方法
计算过程: 1.$g_{t} \leftarrow \Delta_{\theta} f_{t}\left(\theta_{t-1}\right)$第t步的梯度计算 2.$m_{t}=\mu * m_{t-1}+(1-\mu) * g_{t}$ 梯度的滑动平均 3.$n_{t}=\nu * n_{t-1}+(1-\nu) * g_{t}^{2}$ 梯度评方的滑动平均 4.$\hat{m}{t}=\frac{m{t}}{1-\mu^{t}}$ 滑动平均的修正 5.$\rho_{t} \leftarrow \rho_{\infty}-2 t \beta_{2}^{t} /\left(1-\beta_{2}^{t}\right)$计算简单移动平均值的最大值 6.如果$rho_{\infty} > 4$ 移动量二阶矩的修正值和方差修正范围 1.$\widehat{n_{t}} \leftarrow \sqrt{n_{t} /\left(1-\beta_{2}^{t}\right)}$ 2.$r_{t} \leftarrow \sqrt{\frac{\left(\rho_{t}-4\right)\left(\rho_{t}-2\right) \rho_{\infty}}{\left(\rho_{\infty}-4\right)\left(\rho_{\infty}-2\right) \rho_{t}}}$ 3.$\theta_{t} \leftarrow \theta_{t-1}-\alpha_{t} r_{t} \widehat{m_{t}} / \widehat{v_{t}}$ 7.如果$rho_{\infty} < 4$ 则使用非自适应动量更新参数 $\theta_{t} \leftarrow \theta_{t-1}-\alpha_{t} \widehat{m_{t}}$ 优缺点:
1
带来更好的性能,但是精调还是不能完全超越SGD
lookhead
思路:
1
通过一些策略来优化当前的优化算法,不改变算法本身
计算过程: 1.通过k次的循环来基于基础的优化器来进行权重的更新计算(faset weights) 2.选择最后一次的更新来作为后面计算的基本 3.基于移动滑动平均来对上述的计算结果进行再计算(slow weights)
优缺点:
1
可以有效的降低方差,对参数敏感度降低,可以实现更快的收敛速度。
ranger:lookhead+Radam
思路i:
1
将lookhead中的基础优化器换为Radam
Sophia
Adaw