RMSNorm
layerNorm计算如下: \(\begin{aligned} &a_i=\sum_{j=1}^m w_{i j} x_j, \quad y_i=f\left(a_i+b_i\right),\\ &\bar{a}_i=\frac{a_i-\mu}{\sigma} g_i, \quad y_i=f\left(\bar{a}_i+b_i\right),\\ &\mu=\frac{1}{n} \sum_{i=1}^n a_i, \quad \sigma=\sqrt{\frac{1}{n} \sum_{i=1}^n\left(a_i-\mu\right)^2} . \end{aligned}\) 第一行表示未经过归一化。第二行表示经过layerNorm,第三行表示均值和方差的计算。 rmsnorm计算如下: \(\bar{a}_i=\frac{a_i}{\operatorname{RMS}(\mathbf{a})} g_i, \quad \text { where } \operatorname{RMS}(\mathbf{a})=\sqrt{\frac{1}{n} \sum_{i=1}^n a_i^2} .\)
AdamW

如上如所示: AdamW相对与Adam的改动是其将权重衰减项从梯度的计算中拿出来直接加在了最后的权重更新步骤上(图式12)。 其提出的动机在于:原先Adam的实现中如果采用了L2权重衰减,则相应的权重衰减项会被直接加在loss里,从而导致动量的一阶与二阶滑动平均均考虑了该权重衰减项(图1式6),而这影响了Adam的优化效果,而将权重衰减与梯度的计算进行解耦能够显著提升Adam的效果。目前,AdamW现在已经成为transformer训练中的默认优化器了。
==为什么要用这些占显存很大的优化器,基本扩大模型参数了四倍==
SwiGLU
GLU
GLU 全称为 Gated Linear Unit,即门控线性单元函数。 公式: \(\begin{aligned} \operatorname{GLU}(x) & =A \otimes \sigma(B) \\ & =(x \cdot W+b) \otimes \sigma(x \cdot V+c) \end{aligned}\) 输入x经过两个独立的卷积或者是MLP层,得到向量A,B,此时,向量A和B的计算公式为$A = x.W+b,B=x.V + c$。然后向量B经过一个sigmod函数之后,$\sigma(B)$中的每个元素都变为0-1之间的值,这就起来到控制信息是否通过的作用。将向量A与之逐元素相乘之后就得到了GLU层的最终输出结果。 GLU正式使用的时候计算公式为$GLU(x) = x \otimes \sigma(g(x))$,其中$g(x)$表示x经过MLP或者卷积的结果。当$\sigma(g(x))$趋于0表示对x阻断,趋于1表示允许x通过。
FFN及其变体
FFN核心是一个升维再降维的过程,公式为:$FFN(x,W_1,W_2,b_1,b_2) = ReLU(xW_1 + b_1)W_2 + b2$。如T5等研究会将其中的偏置项去除$FFN(x,W_1,W_2) = ReLU(xW_1)W_2$。将其中的ReLU替换为GeLU或者Swish后就得到两种新的FFN \(FFN_{GeLU}(x,W_1,W_2) = ReLU(xW_1)W_2 \\ FFN_{Swish}(x,W_1,W_2) = ReLU(xW_1)W_2\)
GLU及其变体
将GLU中的sigmod函数替换或者去除就衍生出下面的变体 \(\begin{gathered} \operatorname{Bilinear}(x, W, V, b, c)=(x W+b) \otimes(x V+c) \\ \operatorname{ReGLU}(x, W, V, b, c)=\operatorname{ReLU}(x W+b) \otimes(x V+c) \\ \operatorname{GEGLU}(x, W, V, b, c)=\operatorname{GELU}(x W+b) \otimes(x V+c) \\ \operatorname{SwiGLU}(x, W, V, b, c, \beta)=\operatorname{Swish}_\beta(x W+b) \otimes(x V+c) \end{gathered}\) 去除偏置后 \(\begin{aligned} & \operatorname{GLU}(x, W, V)=\sigma(x W) \otimes(x V) \\ & \operatorname{Bilinear}(x, W, V)=(x W) \otimes(x V) \\ & \operatorname{ReGLU}(x, W, V)=\operatorname{ReLU}(x W) \otimes(x V) \\ & \operatorname{GEGLU}(x, W, V)=\operatorname{GELU}(x W) \otimes(x V) \\ & \operatorname{SwiGLU}(x, W, V, \beta)=\operatorname{Swish}_\beta(x W) \otimes(x V) \end{aligned}\)
FFN变体和GLU变体结合
将GLU变体替换FFN的第一层MLP和激活函数,就可以得到新的FFN公式 \(\begin{aligned} & \operatorname{FFN}_{\text {GLU }}(x, W, V)=[\sigma(x W) \otimes(x V)] W_2 \\ & \operatorname{FFN}_{\text {Bilinear }}(x, W, V)=[(x W) \otimes(x V)] W_2 \\ & \operatorname{FFN}_{\text {ReGLU }}(x, W, V)=[\operatorname{ReLU}(x W) \otimes(x V)] W_2 \\ & \operatorname{FFN}_{\text {GEGLU }}(x, W, V)=[\operatorname{GELU}(x W) \otimes(x V)] W_2 \\ & \operatorname{FFN}_{\text {SwiGLU }}(x, W, V)=[\operatorname{Swish}(x W) \otimes(x V)] W_2 \end{aligned}\) 实验验证中,PaLM和LLaMA使用的是$FFN_{SwiGLU}$ ###SwiGLU替换之后的维度 原始FFN层的两层参数分别为h4h和4hh ,总量为$8h^2$。SwiGLU的公式为 \(\operatorname{FFN}_{\text {SwiGLU }}(x, W, V)=[\operatorname{Swish}(x W) \otimes(x V)] W_2\) 从公式上可知,矩阵W和V的维度相同,作用是对x进行升维,W2是降维到原始维度,所以W,V,W2的维度分别为$(h,\alpha h),(h, \alpha h),(\alpha h, h)$总量为$3\alpha h^2$为了保持参数量的不变,$8h^2 = 3\alpha h^2,\alpha = 8/3$。
all_reduce
分布式训练一般分为同步训练和异步训练,同步训练中所有的worker读取mini-batch的不同部分,同步计算损失函数的gradient,最后将每个worker的gradient整合之后更新模型。异步训练中每个worker独立读取训练数据,异步更新模型参数。通常同步训练利用AllReduce来整合不同worker计算的gradient,异步训练则是基于参数服务器架构(parameter server)。
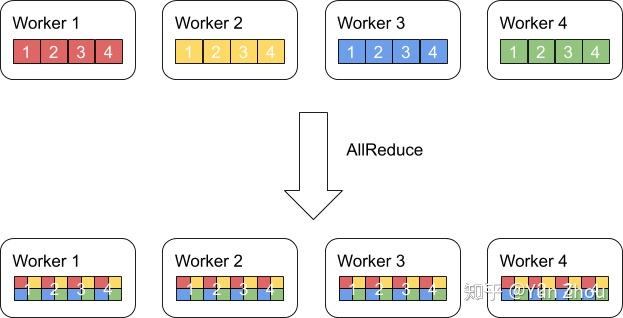
AllReduce其实是一类算法,目标是高效得将不同机器中的数据整合(reduce)之后再把结果分发给各个机器。在深度学习应用中,数据往往是一个向量或者矩阵,通常用的整合则有Sum、Max、Min等。图一展示了AllReduce在有四台机器,每台机器有一个长度为四的向量时的输入和输出。
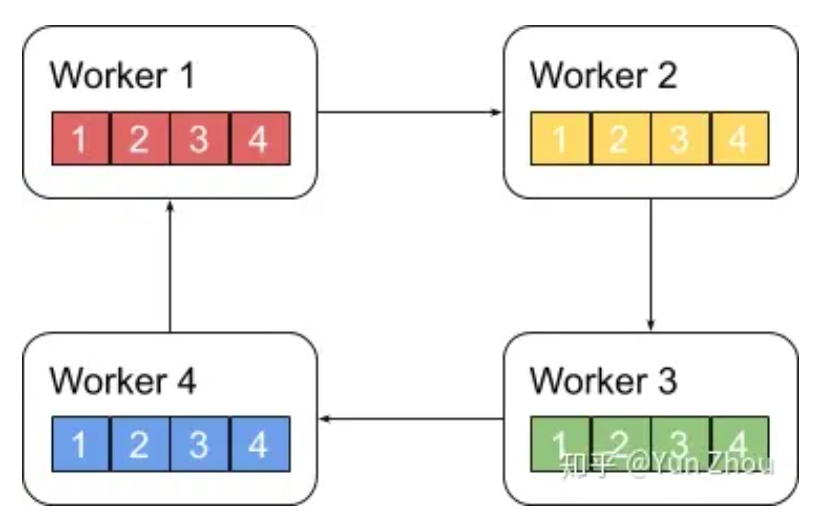
ring allreduce算法分为两个阶段: 第一阶段,将N个worker分布在一个环上,并且把每个worker的数据分成N份。
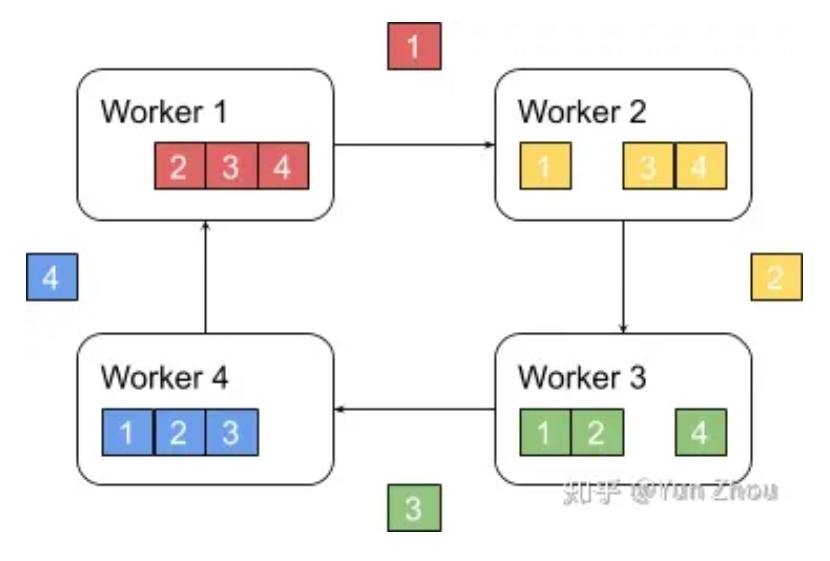
接下来我们具体看第k个worker,这个worker会把第k份数据发给下一个worker,同时从前一个worker收到第k-1份数据。
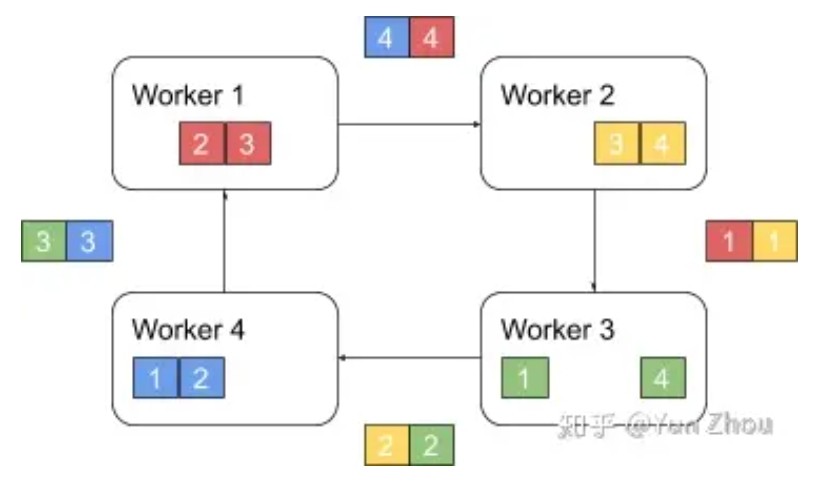
之后worker会把收到的第k-1份数据和自己的第k-1份数据整合,再将整合的数据发送给下一个worker。
以此循环N次之后,每一个worker都会包含最终整合结果的一份。
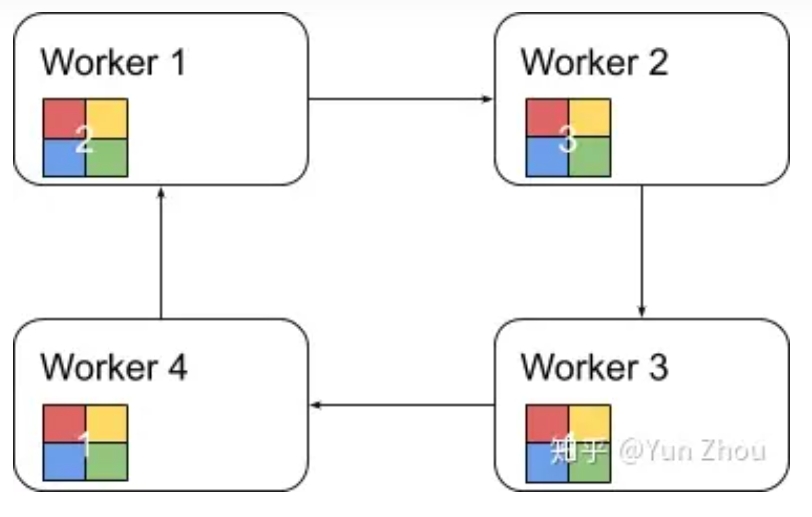
第二阶段,每个worker将整合好的部分发送给下一个worker。worker在收到数据之后更新自身数据对应的部分即可。
假设每个worker的数据是一个长度为S的向量,那么个Ring AllReduce里,每个worker发送的数据量是O(S),和worker的数量N无关。这样就避免了主从架构中master需要处理O(S*N)的数据量而成为网络瓶颈的问题。