为什么需要高效微调
自然语言处理的任务中,从bert出现之后,基本的流程就是预训练+微调。微调需要针对每个下游任务来进行,同时微调后的模型和原始模型是一样大的。这种形式对于bert、gpt来说还勉强可以接受,但是对于再大的模型如gpt3(175B)等就是一个很大的挑战了。 所以我们需要一些可以快速的微调类似gpt3类的大模型,同时也不需要太多的存储。
Adapter Tuning
2019年谷歌提出Parameter-Efficient Transfer Learning for NLP提出针对bert的微调。
出发点:针对特定的下游任务通过全参微调过于低效,如果固定预训练模型的某些层又难以达到好的效果,于是提出Adapter结构。
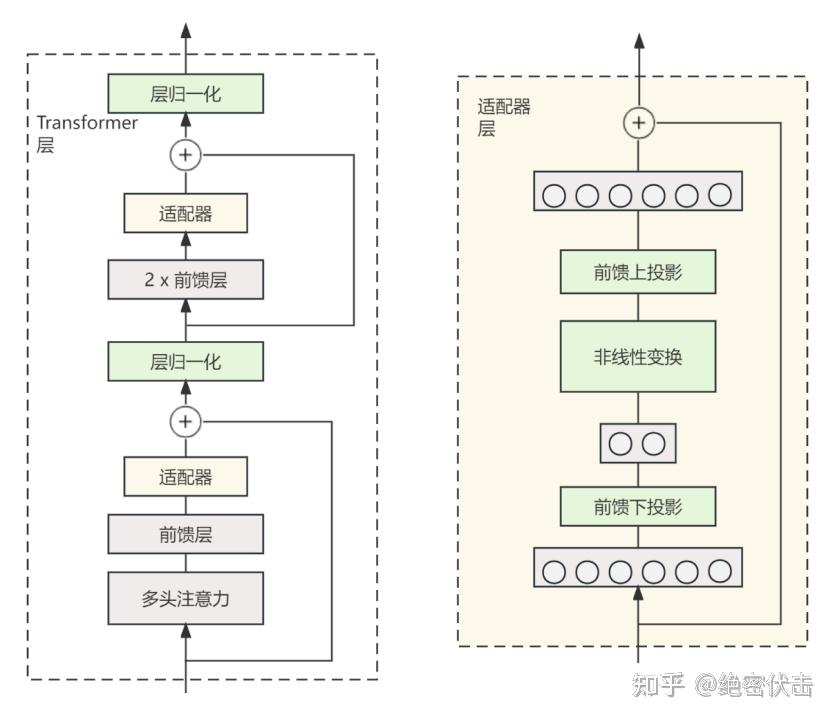
将Adapter嵌入到Transformer中,训练时固定原模型参数,只对新增的结构进行调节。
1
2
3
1. 首先是一个 down-project 层将高维度特征映射到低维特征
2. 然后过一个非线形层之后,再用一个 up-project 结构将低维特征映射回原来的高维特征
3. 同时也设计了 skip-connection 结构,确保了在最差的情况下能够退化为identity(类似残差结构)
==感觉和lora时差不多的东西,只是一个是加旁路,一个是内置?==
Prefix Tuning
2021年斯坦福Prefix-Tuning: Optimizing Continuous Prompts for Generation
与全参数微调不同,是在输入侧构造一段和任务相关的virtual tokens作为prefix,训练中只更新这部分参数。
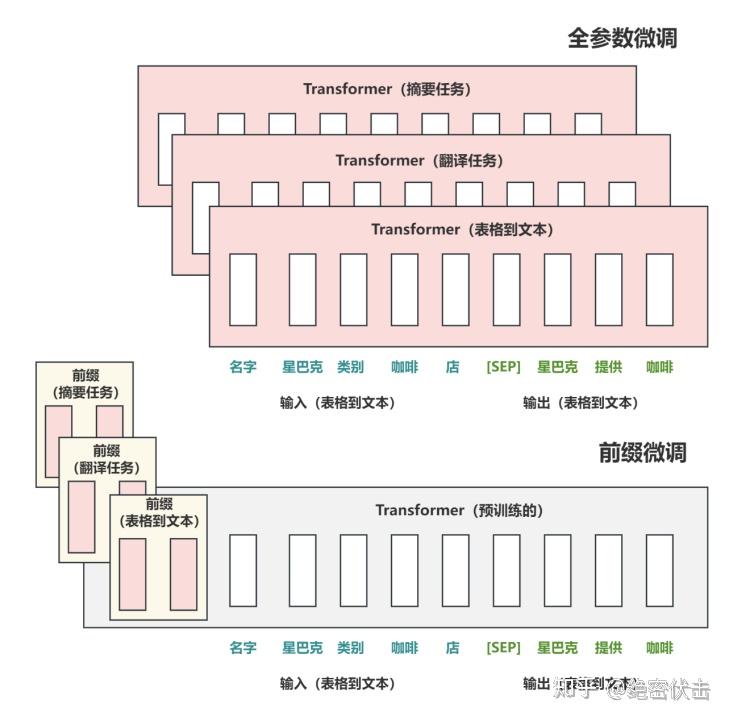
同时,为了防止直接更新 Prefix 的参数导致训练不稳定的情况,在Prefix层前面加MLP 结构(相当于将Prefix分解为更小维度的Input与MLP的组合后输出的结果),训练完成后,只保留Prefix的参数。
prompt tuning
2021年谷歌The Power of Scale for Parameter-Efficient Prompt Tuning prefix tuning的简化版本,只在输入层加入prompt tokens,同时不加MLP解决训练难的问题。==只要模型足够大,不存在这个问题==
固定预训练参数,为每一个任务额外添加一个或多个 embedding,之后拼接 query 正常输入 LLM,并只训练这些 embedding。左图为单任务全参数微调,右图为 Prompt tuning。
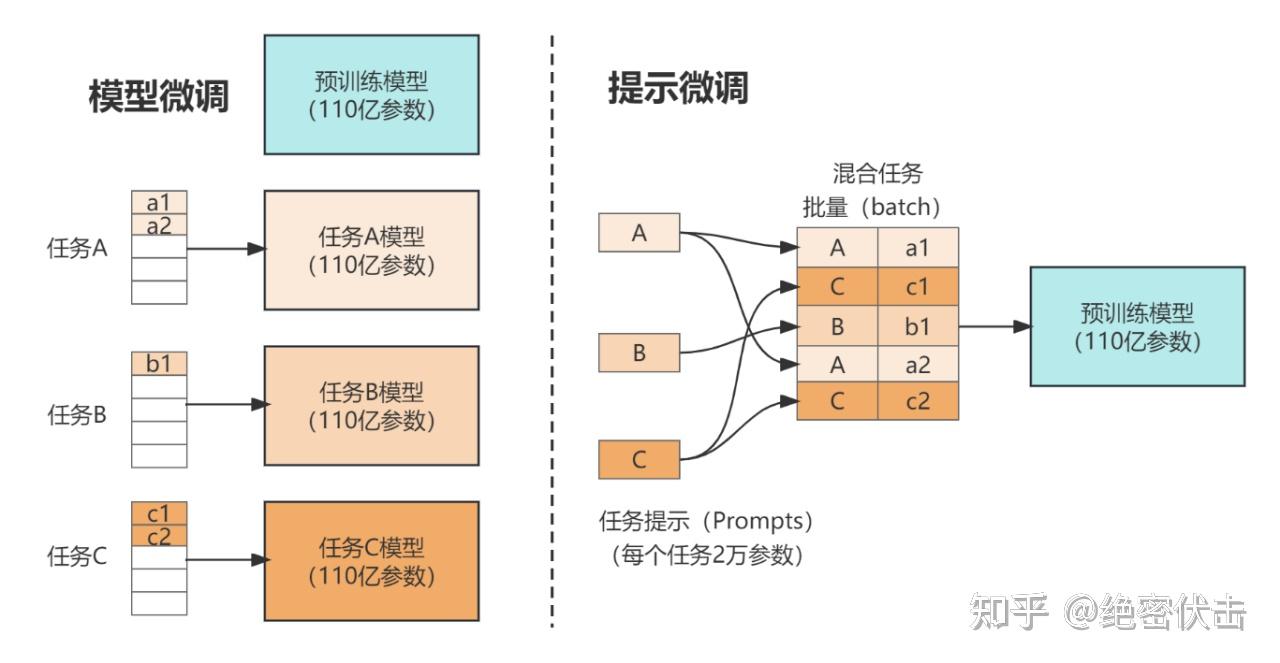
结论:
1
2
3
4
5
1. Prompt 长度影响:模型参数达到一定量级时,Prompt 长度为1也能达到不错的效果,Prompt 长度为20就能达到极好效果。
2. Prompt初始化方式影响:Random Uniform 方式明显弱于其他两种,但是当模型参数达到一定量级,这种差异也不复存在。
3. 预训练的方式:LM Adaptation 的方式效果好,但是当模型达到一定规模,差异又几乎没有了。
4. 微调步数影响:模型参数较小时,步数越多,效果越好。同样随着模型参数达到一定规模,zero shot 也能取得不错效果。
5. 当参数达到100亿规模与全参数微调方式效果无异。
p-tuningv1
P-Tuning方法的提出主要是为了解决这样一个问题:大模型的 Prompt 构造方式严重影响下游任务的效果。
P-tuning重新审视了关于模版的定义,放弃了“模版由自然语言构成”这一常规要求,从而将模版的构建转化为连续参数优化问题,虽然简单,但却有效。
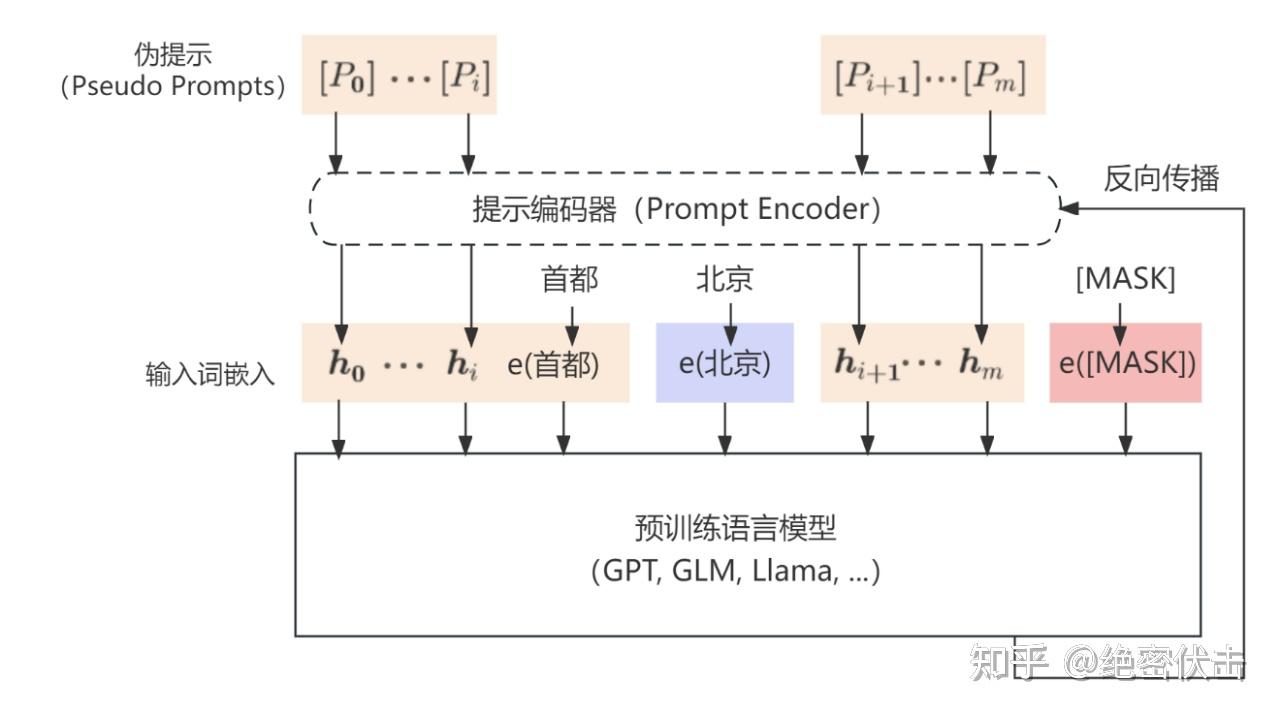
P-Tuning 提出将Prompt转换为可以学习的 Embedding 层,只是考虑到直接对Embedding参数进行优化会存在这样两个挑战:
1
2
Discretenes:对输入正常语料的Embedding层已经经过预训练,而如果直接对输入的prompt embedding进行随机初始化训练,容易陷入局部最优。
Association:没法捕捉到prompt embedding之间的相关关系。
作者在这里提出用 MLP + LSTM 的方式来对 prompt embedding 进行一层处理.P-tuning 依然是固定 LLM 参数,利用多层感知机和 LSTM 对 Prompt 进行编码,编码之后与其他向量进行拼接之后正常输入 LLM。注意,训练之后只保留 Prompt 编码之后的向量即可,无需保留编码器。 P-Tuning 和 Prefix-Tuning 差不多同时提出,做法其实也有一些相似之处,主要区别在:
1
2
1. Prefix Tuning是将额外的embedding加在开头,看起来更像是模仿Instruction指令;而P-Tuning的位置则不固定。
2. Prefix Tuning通过在每个Attention层都加入Prefix Embedding来增加额外的参数,通过MLP来初始化;而P-Tuning只是在输入的时候加入Embedding,并通过LSTM+MLP来初始化。
p-tuningv2
P-Tuning 的问题是在小参数量模型上表现差.于是就有了v2版本P-Tuning v2: Prompt Tuning Can Be Comparable to Fine-tuning Universally Across Scales and Tasks
p Tuning缺陷:
1
2
1. 不同模型规模:Prompt Tuning和P-tuning这两种方法都是在预训练模型参数规模够足够大时,才能达到和Fine-tuning类似的效果,而参数规模较小时效果则很差。
2. 不同任务类型:Prompt Tuning和P-tuning这两种方法在sequence tagging 任务上表现都很差。
相比 Prompt Tuning 和 P-tuning 的方法, P-tuning v2 方法在多层加入了 Prompts tokens 作为输入,带来两个方面的好处:
1
2
1. 带来更多可学习的参数(从P-tuning和Prompt Tuning的0.1%增加到0.1%-3%),同时也足够parameter-efficient。
2. 加入到更深层结构中的Prompt能给模型预测带来更直接的影响。
==注意== prefix tuning在所有layer都加入了prompt,而P-Tuning只在输入层。P-Tuning V2在所有层都加入了prompt,和prefix tuning的区别在于P-Tuning V2每一层的prompt是独立的,并不是由上一层计算得来。
lora
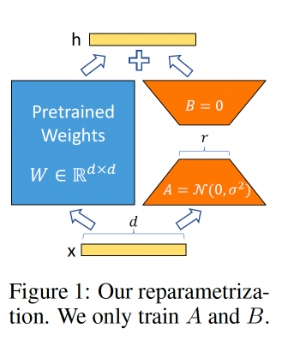
lora提出的依据:模型是过参数化的,它们有更小的内在维度,模型主要依赖于这个低的内在维度(low intrinsic dimension)去做任务适配。
基础
思路:
- 在原模型侧边增加旁路,做降维升维的操作来模拟内在维度。
- 固定原模型,只训练图中的AB矩阵。
- A初始化高斯分布,B初始化全0(保证训练开始时旁路维0)
假设需要微调一个语言模型,需要对其参数进行更新,权重表示为$W_0+\triangle W$ ,其中$W_0$表示预训练语言的参数,$triangle W$表示需要更新的参数。如果是全量微调则微调的参数和语言模型参数一样。
而如果微调方式切换到lora的话,需要的参数如下: 首先预训练模型的参数为$W_0 \in R^{d*k}$ 进而参数更新可以转换为: \(W_0 + \triangle W = W_0 + BA, B \in R^{d*r} , A \in R^{d*r}\) 训练过程中只需要调节A和B的参数就可以。前向计算为: \(h = W_0x+ \triangle W x = W_0 x +BAx = (W_0 + AB)x\)
==A矩阵不能全0初始化,B矩阵可全0初始化== 对于$h = W_0x + BAx$ ,假设$h^{()2}$,则: \(h_i^{(2)}=\sum_j z_{i, j} x_j=\sum_j\left(\sum_k B_{i, k} A_{k, j}\right) x_j\)
训练策略
加入学习率调度器通常可以稳定训练,余弦退火是一种常用的学习率调度器,首先从一个较高的学习率开始平滑递减,以一种类似余弦函数的方式逼近零点,在使用的时候通常是半周期的变体,即在训练过程中只完成半个余弦周期,如下图所示:
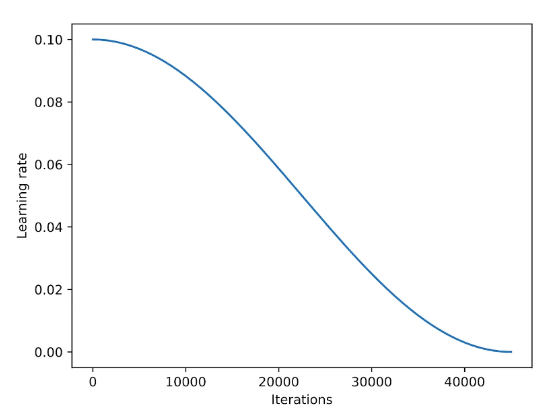
经验:对于SGD提升比较明显,但是对Adam,AdamW影响较小。
==?为什么不使用SGD作为优化函数,其相对Adam等优化器节省了多余参数的存储,可以降低对GPU显存的使用==
对数据循环多次使用,并不会提升性能,相反可能会导致结果的恶化。
lora在前向传播的时候引入了扩展系数,用于将lora的权重应用于预训练权重,涉及到的参数有r,alpha。具体计算为$scaling = alpha / r$,$weight += (lora_b @ lora_a) * scaling$。
通常设置r 为alpha的一半性能较好,但是对一些特定数据集也可能有更好的经验参数。
学习率设置3e-4,梯度累积的使用,weight_decay=0.1,warmup_steps=100 如果是SGD的话,学习率0.1。动量0.9
qlora
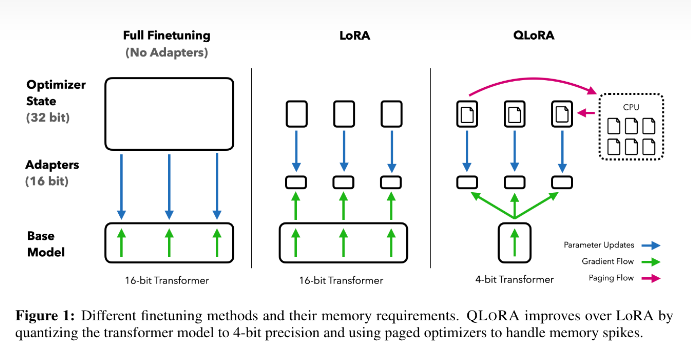
论文 创新点:
1
2
3
1. 一种新的数据类型4位NormalFloat
2. 双重量化以减少平均内存占用
3. 分页优化器来管理内存高峰
计算流程:
- 一个基本模型权重的存储数据类型NF4。
- 一个用语执行计算的数据类型BF16。
- 权重从存储的数据类型反量化位计算数据类型以执行前向后向传递。
- 传递过程中仅计算使用BF16的LoRA参数的权重梯度。
- 权重在需要时解压缩,所以在训练和推理期间内存使用量保持较低。
Quantize
模型的大小通常由其参数的数量及其精度决定,常见的精度有全精度float32(FP32)、半精度float16(FP16)和bfloat16(BF16)。
FP32:单精度浮点数,用8bit 表示指数,23bit 表示小数。使用此数据类型,可以表示各种浮点数,并且支持大多硬件。 FP16:半精度浮点数,用5bit 表示指数,10bit 表示小数。FP16 表示整数范围较小,但是尾数精度较高。 BF16:是对FP32单精度浮点数截断数据,用8bit 表示指数,7bit 表示小数。BF16 可表示的整数范围与FP32一样广泛。但只有新的硬件(A100\3090\4090等)才支持,V100/昇腾910等不支持

量化的本质实际是从一种数据类型舍入到另一种数据类型,通常包含量化和反量化两步: 假如我们有两组数据类型A、B,A可以表示的数值为[0, 1, 2, 3, 4, 5],B可以表示的数值为[0, 2, 4]。我们要做的便是:
1
2
3
4
5
6
7
8
9
将数据范围从A标准化为B。数据类型A表示的向量为[3, 1, 2, 3]。
找到向量[3, 1, 2, 3]的最大绝对值3
向量[3, 1, 2, 3]除以最大值3:[3, 1, 2, 3]->[1, 0.33, 0.66, 1.0]
将向量[1, 0.33, 0.66, 1.0]与B的数据范围4相乘:[1, 0.33, 0.66, 1.0]->[4.0, 1.33, 2.66, 4.0]
将向量[4.0, 1.33, 2.66, 4.0]中的每个值用B中最接近的数值表示:[4.0, 1.33, 2.66, 4.0] -> [4, 2, 2, 4]。
用B中最接近的数值表示A 。
[4, 2, 2, 4]除以4->[1.0, 0.5, 0.5, 1.0]
乘以量化过程中找到的最大的绝对值:[1.0, 0.5, 0.5, 1.0] -> [3.0, 1.5, 1.5, 3.0]
近似表示:[3.0, 1.5, 1.5, 3.0] -> [3, 2, 2, 3]
==注意经过量化和反量化之后会存在一定的精度误差,解决方法是使用更多的量化参数:比如不同的区间使用不同的独立的量化参数==
借鉴LLM.int8中的vector-wise想量化+混合精度分解。
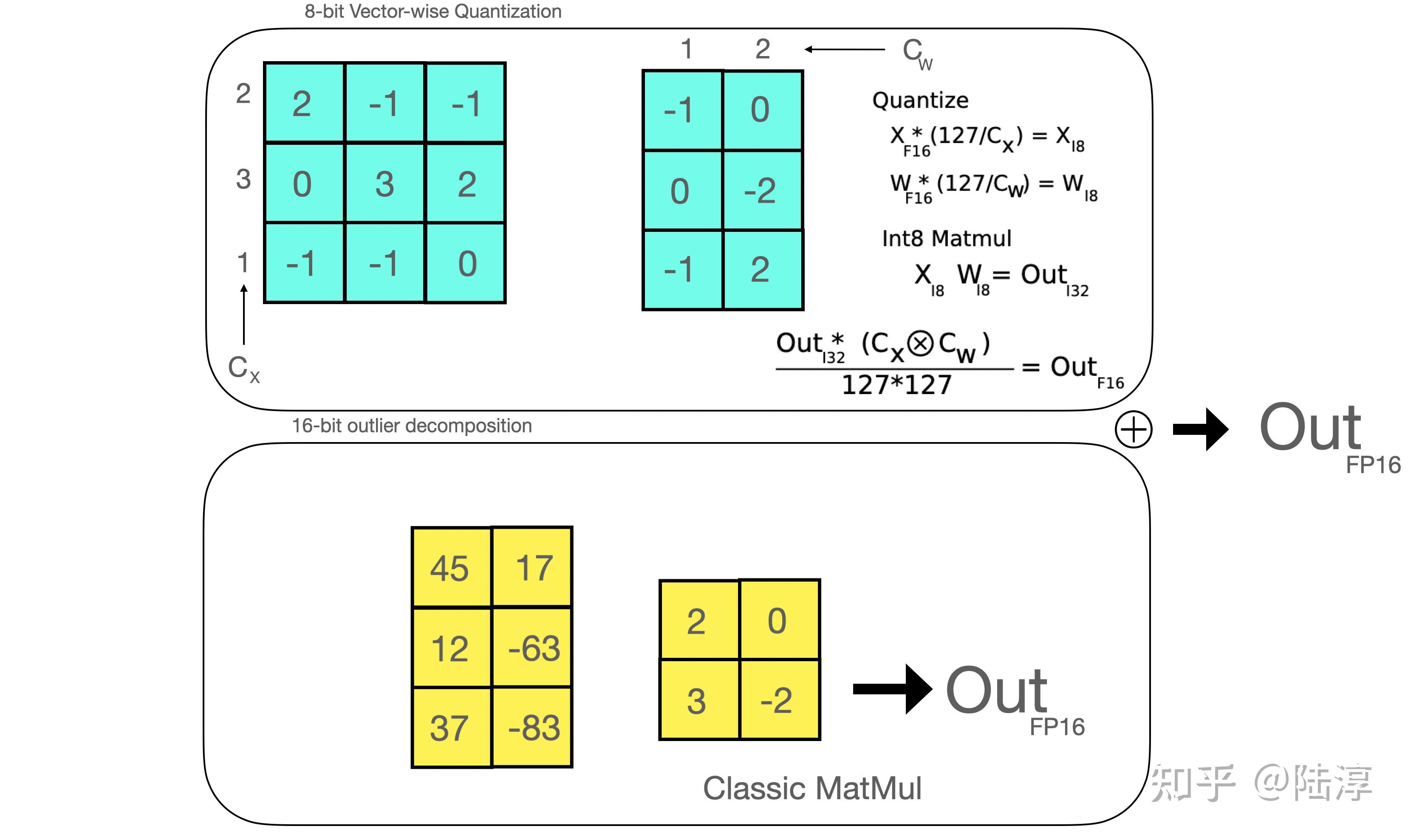
如上图所示:先找到离群点,离群点通过fp16计算,其他的通过int8量化计算,最终再反量化回去和离群点相加处理。
4-bit NormalFloat
是一种建立在分位数量化技术的基础之上的一种信息理论上最优的数据类型。 对于预训练的神经网络的权重来说通常具有标准差位0的正态分布性质,所以我们可以通过缩放系数来将所有的权值改为固定期望值,从而使得该分布适合我们的数据类型范围,一旦权重范围和数据类型范围匹配,我们就可以进行了量化了。
分位数量化技术的主要思想便是将数值尽量落到均值为0,标准差为[-1,1]的正态分布的固定期望值上。离群值对于模型量化的影响极其重要,而由于分位数估计算法的近似性质,精度量化对于离群值又有很大的误差。分位数量化技术使得每个量化分区中具有相等的期望值,相等的期望值可以避免昂贵的分位数估计和近似误差,使得精确的分位数估计在计算上可行。
分位数量化步骤:
- 估计N(0,1)分布的$2^{k+1}$个分位数,得到正太分布的k-bit位量化数据类型。
- 将其值归一化到[-1,1]范围内。
- 通过absmax来重新缩放权重张量的标准差,以获得k-bit的数据形式。 分位数$q_i$的计算过程: \(q_i = 1/2((Q_x(i/(z^k +1))) + Q_X((1+i)/(2^k + 1)))\) 它在量化过程中保留了零点,并使用所有$2^k$位来表示k-bit数据类型。这种数据类型通过估计两个范围的分位数$q_i$来创建一个非对称的数据类型,这两个范围分别是负数部分[-1,0]的$r « min(d, k)$和正数部分[0,1]的$2^{k-1}+1$ 。然后,它统一了这两组分位数$q_i$,并从两组中都出现的两个零中移除一个。这种结果数据类型在每个量化bin中都有相等的期望值数量,因此被称为$2^{k-1}+1$。
以NF4,即k=4为例,标准正态分布量化函数把[-1, 0]分成7份,然后生成[-1, …, 0]共8个分位数, 把[0, 1]分成8份,然后生成[0, …, 1]共9个分位数,两个合起来去掉一个0就生成全部的16个分位数了。
1
我们的目标是找到等面积的量化区间,使得量化区间左右两侧的面积相等。这意味着我们不从正态分布的0和1量化区间开始,而是从一个偏移量量化区间开始。代码片段中称之为"offset",其值为1-1/(215)。如果我们有一个非对称的数据类型,其中一侧的间隔等于每个量化区间周围的16个“半个”,而另一侧只有15个“半个”。因此,平均偏移量为(1-1/(2*15) + 1-1/(2*16))/2 = 0.9677083。
Double Quantization
Double Quantization是将额外的量化常数进行二次量化以减小内存开销的过程。例如每64个参数块共享一个32bit的量化常数, 这样的话相当于每一个参数的量化额外开销为32/64 = 0.5 bit。这个总体来说也是比较大的一个开销,所以为了进一步优化这个量化开销,我们对其进行二次量化(Double Quantization),即把第一次32bit量化的输出作为第二次量化的输入,我们采用256的块大小对量化常数进行FP8量化,这样的话,我们可以把每个参数的量化额外开销降低到:8/16 + 32/(64*256) = 0.127bit.
Paged Optimizers
使用NVIDIA统一内存功能,该功能在CPU和GPU之间进行自动page对page传输,以便在GPU偶尔OOM的情况仍然下进行模型训练和微调。 可以理解成显存偶发OOM时,QLoRA会将优化器状态自动的驱逐到CPU RAM,当在优化器更新步骤中需要内存时,它们会被分页回GPU内存,从而保证训练正常训练下去。